Or you want a quick look: Lý thuyết bài 4: Đường trung bình của tam giác, của hình thang
Giải bài tập SGK Toán 8 trang 79, 80 giúp các em học sinh lớp 8 xem gợi ý giải các bài tập của Bài 4: Đường trung bình của tam giác, của hình thang Hình học 8 Chương 1. Qua đó các em sẽ nhanh chóng hoàn thiện toàn bộ bài tập của bài 4 Chương I Hình học 8 tập 1.
Lý thuyết bài 4: Đường trung bình của tam giác, của hình thang
1. Đường trung bình của tam giác
– Định lí 1: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba.
– Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
– Định lí 2: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
2. Đường trung bình của hình thang
– Định lí 3: Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai
– Định nghĩa: Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.
– Định lí 4: Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.
Giải bài tập toán 8 trang 79, 80 tập 1
Bài 20 (trang 79 SGK Toán 8 Tập 1)
Tính x trên hình 41.
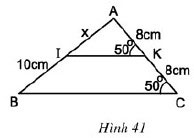
Gợi ý đáp án:
Tam giác ABC có:
Mà
Nên BC // IK
Mặt khác KA = KC = 8, có nghĩa K là trung điểm của AC.
Theo định lí 1 về đường trung bình của tam giác thì I cũng là trung điểm của AB
Suy ra IA = IB
Mà IB = 10 nên IA = 10
Vậy x = 10cm
Bài 21 (trang 79 SGK Toán 8 Tập 1)
Tính khoảng cách AB giữa hai mũi của compa trên hình 42, biết rằng C là trung điểm của OA, D là trung điểm của OB và CD = 3cm
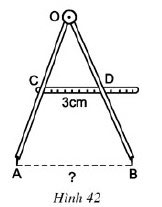
Gợi ý đáp án:
Ta có:
⇒ CD là đường trung bình của
Do đó
Vậy khoảng cách giữa hai mũi compa là 6cm
Bài 22 (trang 80 SGK Toán 8 Tập 1)
Cho hình 43. Chứng minh rằng AI = IM.
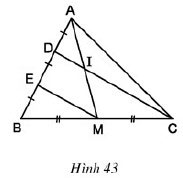
Gợi ý đáp án:
Tam giác BDC có:
⇒ CD là đường trung bình của
Do đó EM // DC ⇒ EM // DI
Tam giác AEM có:
⇒ AI = IM (đpcm)
Bài 23 (trang 80 SGK Toán 8 Tập 1)
Tính x trên hình 44.
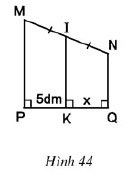
Gợi ý đáp án:
Tứ giác MNQP có:
⇒ MP//NQ
Do đó: tứ giác MNQP là hình thang.
Mặt khác:
⇒ IK//MP
Mà IM = IN
Nên IK là đường trung bình của hình thang MNQP
Suy ra KQ = KP = 5
Vậy x = 5dm
Bài 24 (trang 80 SGK Toán 8 Tập 1)
Hai điểm A và B thuộc cùng một nửa mặt phẳng có bờ là đường thẳng xy. Khoảng cách từ điểm A đến xy bằng 12cm, khoảng cách từ điểm B đến xy bằng 20cm. Tính khoảng cách từ trung điểm C của AB đến xy.
Gợi ý đáp án:
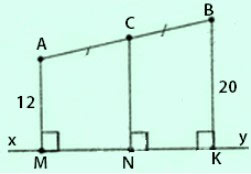
Kẻ
Khi đó ta có: AM//CN//BK ⇒ ABKM là hình thang.
Mặt khác ta có CA = CB (gt)
Suy ra CN là đường trung bình của hình thang ABKM
Do đó:
Vậy khoảng cách từ trung điểm C của AB đến đường thẳng xy là 16cm.
Bài 25 (trang 80 SGK Toán 8 Tập 1)
Hình thang ABCD có đáy AB, CD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, BD. Chứng minh ba điểm E, K, F thẳng hàng.
Gợi ý đáp án:
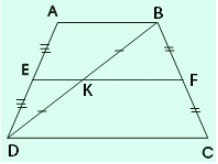
Tam giác ABD có:
⇒ EK là đường trung bình của
Suy ra EK //AB
Mặt khác AB//CD (gt)
Suy ra EK//CD (1)
Tam giác BDC có:
⇒ KF là đường trung bình của
Suy ra KF//DC (2)
Theo tiên đề Ơclit, từ (1) và (2) suy ra ba điểm E, K, F thẳng hàng.
Giải bài tập toán 8 trang 80 tập 1: Luyện tập
Bài 26 (trang 80 SGK Toán 8 Tập 1)
Tính x, y trên hình 45, trong đó: AB//CD//EF//GH
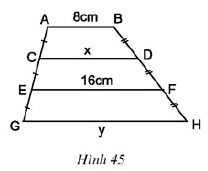
Gợi ý đáp án:
Ta có AB//EF nên ABFE là hình thang
⇒ AD là đường trung bình của hình thang ABFE
Do đó:
Vậy x = 12cm
Tương tự ta có CD//GH nên CDHG là hình thang.
⇒ EF là đường trung bình của hình thang CDHG
Do đó:
Vậy y = 20cm
Bài 27 (trang 80 SGK Toán 8 Tập 1)
Cho tứ giác ABCD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, AC
a) So sánh các độ dài EK và CD, KF và AB
b) Chứng minh rằng
Gợi ý đáp án:
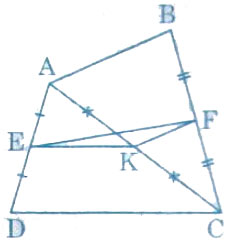
a) Ta có
⇒ EK là đường trung bình của tam giác ACD
Do đó
Tương tự ta có:
⇒ KF là đường trung bình của tam giác ABC
Do đó
b) Trong tam giác EFK ta có:
Bài 28 (trang 80 SGK Toán 8 Tập 1)
Cho hình thang ABCD (AB//CD), E là trung điểm của AD, F là trung điểm của BC. Đường thẳng EF cắt BD ở I, cắt AC ở K
a) Chứng minh rằng AK = KC, BI = ID
b) Cho AB = 6cm, CD = 10cm. Tính các độ dài EI, KF, IK
Gợi ý đáp án:
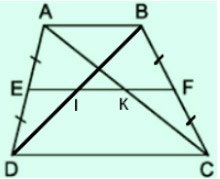
a) Ta có:
⇒ EF là đường trung bình của hình thang ABCD.
Do đó EF // AB // CD
Tam giác ABC có:
Tam giác ABD có:
b) Ta có:
EF là đường trung bình của hình thang ABCD nên:
EI là đường trung bình của tam giác ABD nên:
KF là đường trung bình của tam giác ABC nên:
Ta cũng có EF = EI + IK + KF
⇒ IK = EF – (EI + KF) = 8 – (3 + 3) = 2
Vậy EI = KF = 3cm, IK = 2cm
Giải bài tập SGK Toán 8 trang 79, 80 giúp các em học sinh lớp 8 xem gợi ý giải các bài tập của Bài 4: Đường trung bình của tam giác, của hình thang Hình học 8 Chương 1. Qua đó các em sẽ nhanh chóng hoàn thiện toàn bộ bài tập của bài 4 Chương I Hình học 8 tập 1.
Lý thuyết bài 4: Đường trung bình của tam giác, của hình thang
1. Đường trung bình của tam giác
– Định lí 1: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba.
– Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
– Định lí 2: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
2. Đường trung bình của hình thang
– Định lí 3: Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai
– Định nghĩa: Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.
– Định lí 4: Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.
Giải bài tập toán 8 trang 79, 80 tập 1
Bài 20 (trang 79 SGK Toán 8 Tập 1)
Tính x trên hình 41.

Gợi ý đáp án:
Tam giác ABC có:
Mà
Nên BC // IK
Mặt khác KA = KC = 8, có nghĩa K là trung điểm của AC.
Theo định lí 1 về đường trung bình của tam giác thì I cũng là trung điểm của AB
Suy ra IA = IB
Mà IB = 10 nên IA = 10
Vậy x = 10cm
Bài 21 (trang 79 SGK Toán 8 Tập 1)
Tính khoảng cách AB giữa hai mũi của compa trên hình 42, biết rằng C là trung điểm của OA, D là trung điểm của OB và CD = 3cm

Gợi ý đáp án:
Ta có:
⇒ CD là đường trung bình của
Do đó
Vậy khoảng cách giữa hai mũi compa là 6cm
Bài 22 (trang 80 SGK Toán 8 Tập 1)
Cho hình 43. Chứng minh rằng AI = IM.

Gợi ý đáp án:
Tam giác BDC có:
⇒ CD là đường trung bình của
Do đó EM // DC ⇒ EM // DI
Tam giác AEM có:
⇒ AI = IM (đpcm)
Bài 23 (trang 80 SGK Toán 8 Tập 1)
Tính x trên hình 44.

Gợi ý đáp án:
Tứ giác MNQP có:
⇒ MP//NQ
Do đó: tứ giác MNQP là hình thang.
Mặt khác:
⇒ IK//MP
Mà IM = IN
Nên IK là đường trung bình của hình thang MNQP
Suy ra KQ = KP = 5
Vậy x = 5dm
Bài 24 (trang 80 SGK Toán 8 Tập 1)
Hai điểm A và B thuộc cùng một nửa mặt phẳng có bờ là đường thẳng xy. Khoảng cách từ điểm A đến xy bằng 12cm, khoảng cách từ điểm B đến xy bằng 20cm. Tính khoảng cách từ trung điểm C của AB đến xy.
Gợi ý đáp án:

Kẻ
Khi đó ta có: AM//CN//BK ⇒ ABKM là hình thang.
Mặt khác ta có CA = CB (gt)
Suy ra CN là đường trung bình của hình thang ABKM
Do đó:
Vậy khoảng cách từ trung điểm C của AB đến đường thẳng xy là 16cm.
Bài 25 (trang 80 SGK Toán 8 Tập 1)
Hình thang ABCD có đáy AB, CD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, BD. Chứng minh ba điểm E, K, F thẳng hàng.
Gợi ý đáp án:

Tam giác ABD có:
⇒ EK là đường trung bình của
Suy ra EK //AB
Mặt khác AB//CD (gt)
Suy ra EK//CD (1)
Tam giác BDC có:
⇒ KF là đường trung bình của
Suy ra KF//DC (2)
Theo tiên đề Ơclit, từ (1) và (2) suy ra ba điểm E, K, F thẳng hàng.
Giải bài tập toán 8 trang 80 tập 1: Luyện tập
Bài 26 (trang 80 SGK Toán 8 Tập 1)
Tính x, y trên hình 45, trong đó: AB//CD//EF//GH

Gợi ý đáp án:
Ta có AB//EF nên ABFE là hình thang
⇒ AD là đường trung bình của hình thang ABFE
Do đó:
Vậy x = 12cm
Tương tự ta có CD//GH nên CDHG là hình thang.
⇒ EF là đường trung bình của hình thang CDHG
Do đó:
Vậy y = 20cm
Bài 27 (trang 80 SGK Toán 8 Tập 1)
Cho tứ giác ABCD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, AC
a) So sánh các độ dài EK và CD, KF và AB
b) Chứng minh rằng
Gợi ý đáp án:

a) Ta có
⇒ EK là đường trung bình của tam giác ACD
Do đó
Tương tự ta có:
⇒ KF là đường trung bình của tam giác ABC
Do đó
b) Trong tam giác EFK ta có:
Bài 28 (trang 80 SGK Toán 8 Tập 1)
Cho hình thang ABCD (AB//CD), E là trung điểm của AD, F là trung điểm của BC. Đường thẳng EF cắt BD ở I, cắt AC ở K
a) Chứng minh rằng AK = KC, BI = ID
b) Cho AB = 6cm, CD = 10cm. Tính các độ dài EI, KF, IK
Gợi ý đáp án:

a) Ta có:
⇒ EF là đường trung bình của hình thang ABCD.
Do đó EF // AB // CD
Tam giác ABC có:
Tam giác ABD có:
b) Ta có:
EF là đường trung bình của hình thang ABCD nên:
EI là đường trung bình của tam giác ABD nên:
KF là đường trung bình của tam giác ABC nên:
Ta cũng có EF = EI + IK + KF
⇒ IK = EF – (EI + KF) = 8 – (3 + 3) = 2
Vậy EI = KF = 3cm, IK = 2cm