Or you want a quick look: Công thức tính diện tích tam giác, chu vi tam giác đầy đủ, chi tiết từ cơ bản đến nâng cao, áp dụng để tính tam giác thường, vuông, cân, đều sẽ có trong bài viết dưới đây.
Công thức tính diện tích tam giác, chu vi tam giác đầy đủ, chi tiết từ cơ bản đến nâng cao, áp dụng để tính tam giác thường, vuông, cân, đều sẽ có trong bài viết dưới đây.
1. Tam giác thường
Tam giác thường là tam giác có độ dài ba cạnh khác nhau và số đo ba góc cũng không bằng nhau.
– Công thức tính diện tích tam giác thường
Tam giác thường có thể bao gồm các trường hợp đặc biệt khác như tam giác cân, tam giác vuông, tam giác đều. Vì thế, có thể áp dụng cùng các công thức dưới đây để tính diện tích cho nhiều tam giác khác nhau.
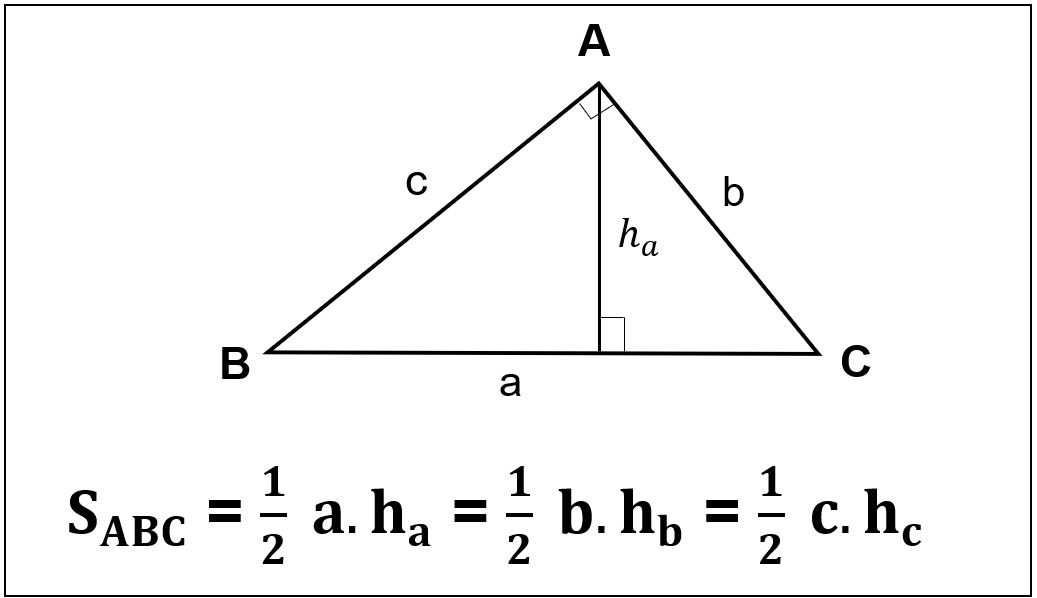
+ Tính diện tích khi biết độ dài đường cao
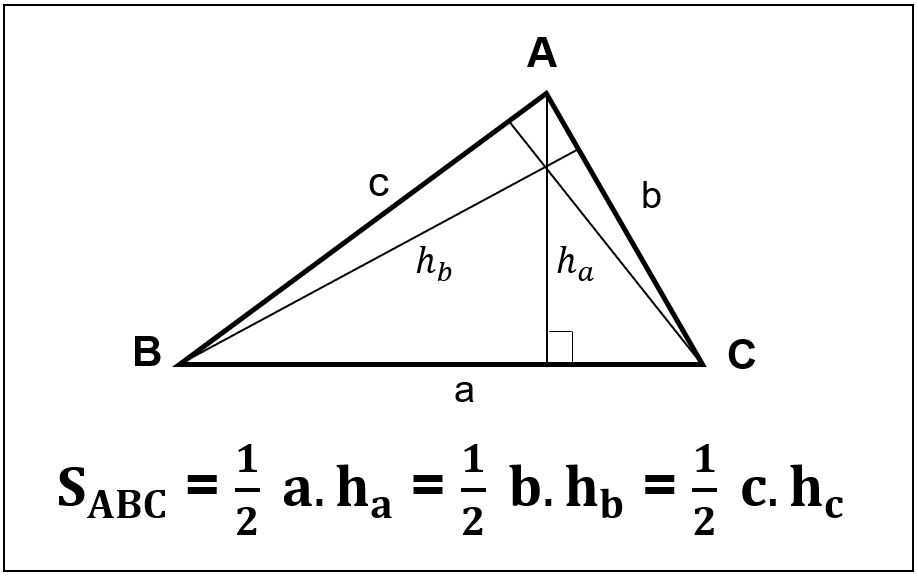
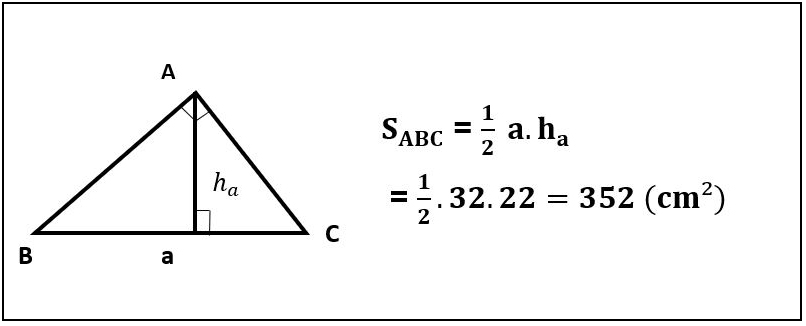
Diện tích tam giác bằng ½ tích đường cao hạ từ đỉnh nhân với cạnh đối diện của đỉnh đó.
Trong đó:
a, b, c: Lần lượt là độ dài các cạnh của tam giác.
ha, hb, hc: Lần lượt là chiều cao được nối từ đỉnh A,B, C.
Bây giờ mình sẽ làm thử một ví dụ cho các bạn hiểu hơn về cách sử dụng công thức này nhé!
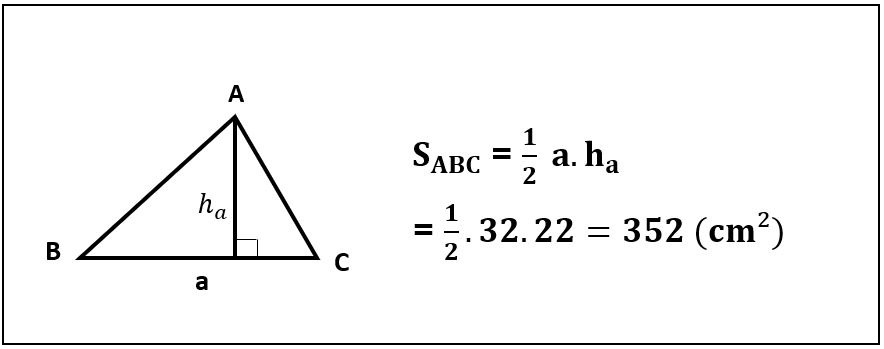
Ví dụ: Tính diện tích tam giác ABC có độ dài cạnh đáy là 32cm và chiều cao là 22cm.
+ Tính diện tích tam giác khi biết một góc
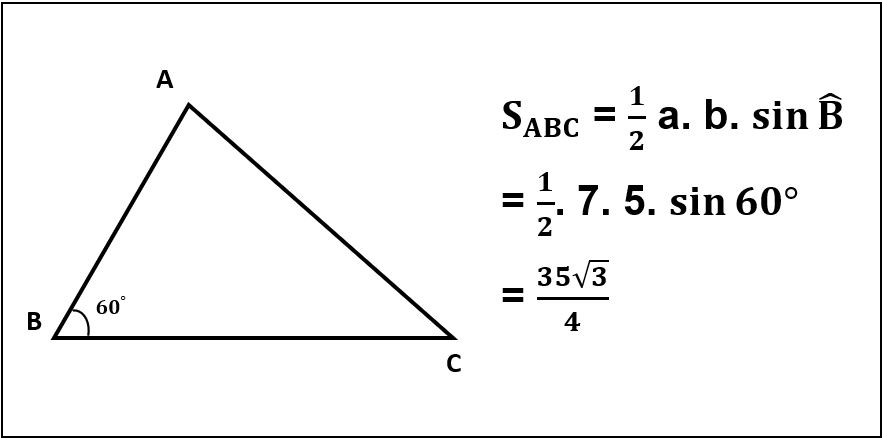
Diện tích tam giác bằng ½ tích hai cạnh kề với sin của góc hợp bởi hai cạnh đó trong tam giác.
Trong đó:
a, b, c: Lần lượt là độ dài các cạnh của tam giác.
Ví dụ: Cho tam giác ABC có góc B bằng 60 độ, cạnh BC = 7, cạnh AB = 5. Tính diện tích tam giác ABC?
Nếu bạn chưa hiểu rõ và biết hết các công thức lượng giác thì hãy xem: Tổng hợp bảng các công thức lượng giác đầy đủ, chi tiết, dễ hiểu để áp dụng thành thạo công thức này.
+ Tính diện tích tam giác sử dụng công thức Heron
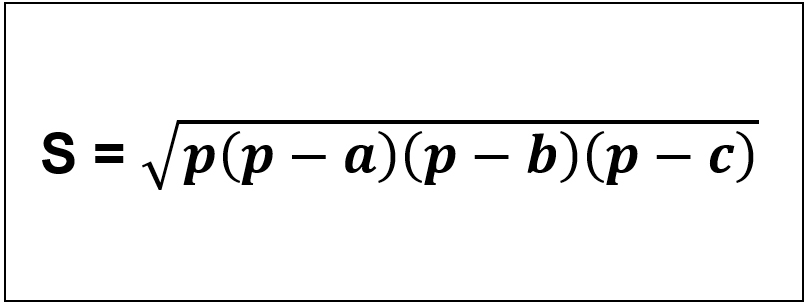
Trong đó:
a, b, c: Lần lượt là độ dài các cạnh của tam giác.
p: Nửa chu vi tam giác, bằng ½ tổng các cạnh của một tam giác.
Ví dụ: Tính diện tích hình tam giác có độ dài cạnh AB = 8, AC = 7, CB = 9.
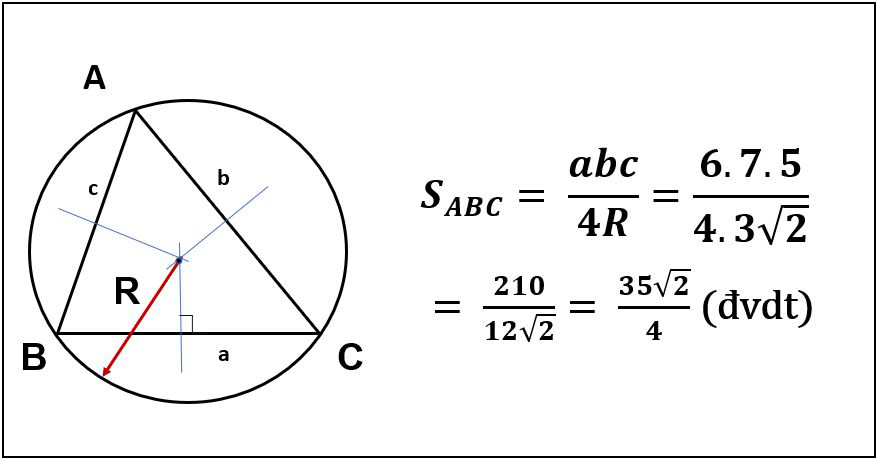
+ Tính diện tích bằng bán kính đường tròn ngoại tiếp tam giác (R)
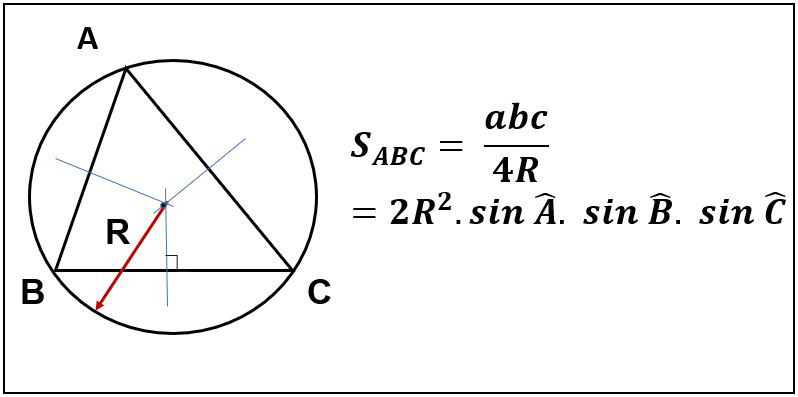
Trong đó:
a, b, c: Lần lượt là độ dài các cạnh của tam giác.
R: Bán kính đường tròn ngoại tiếp.
Ví dụ: Cho tam giác ABC, độ dài các cạnh a = 6, b = 7, c = 5, R = 3 (R là bán kính đường tròn ngoại tiếp tam giác ABC).
+ Tính diện tích bằng bán kính đường tròn nội tiếp tam giác (r)
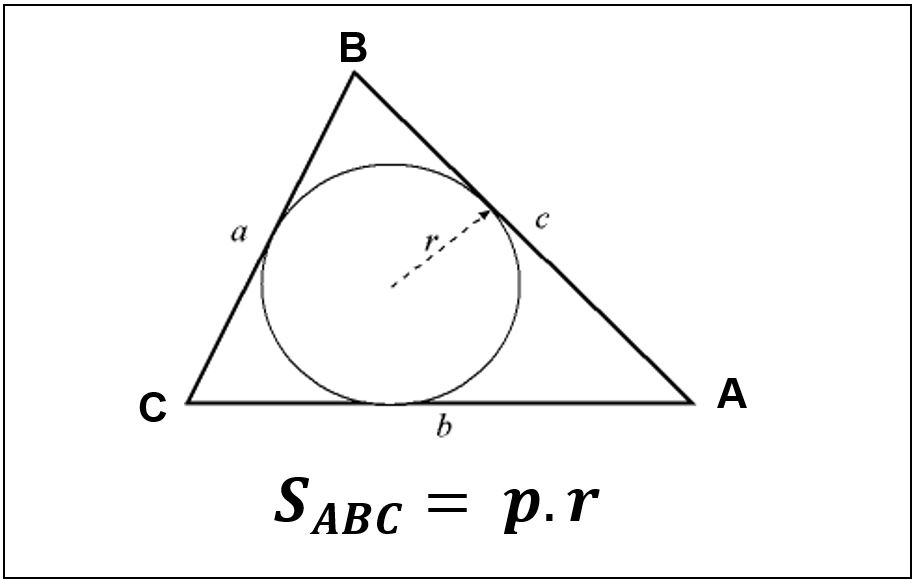
Trong đó:
p: Nửa chu vi tam giác.
r: Bán kính đường tròn nội tiếp.
Ví dụ: Tính diện tích tam giác ABC biết độ dài các cạnh AB = 20, AC = 21, BC = 15, r = 5 (r là bán kính đường tròn nội tiếp tam giác ABC).
– Công thức tính chu vi tam giác thường
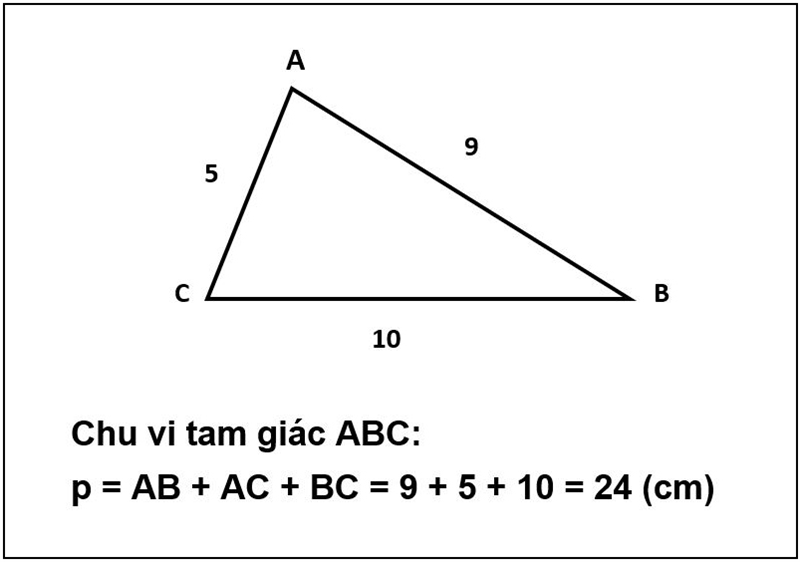
Chu vi hình tam giác thường bằng tổng độ dài ba cạnh tam giác đó:
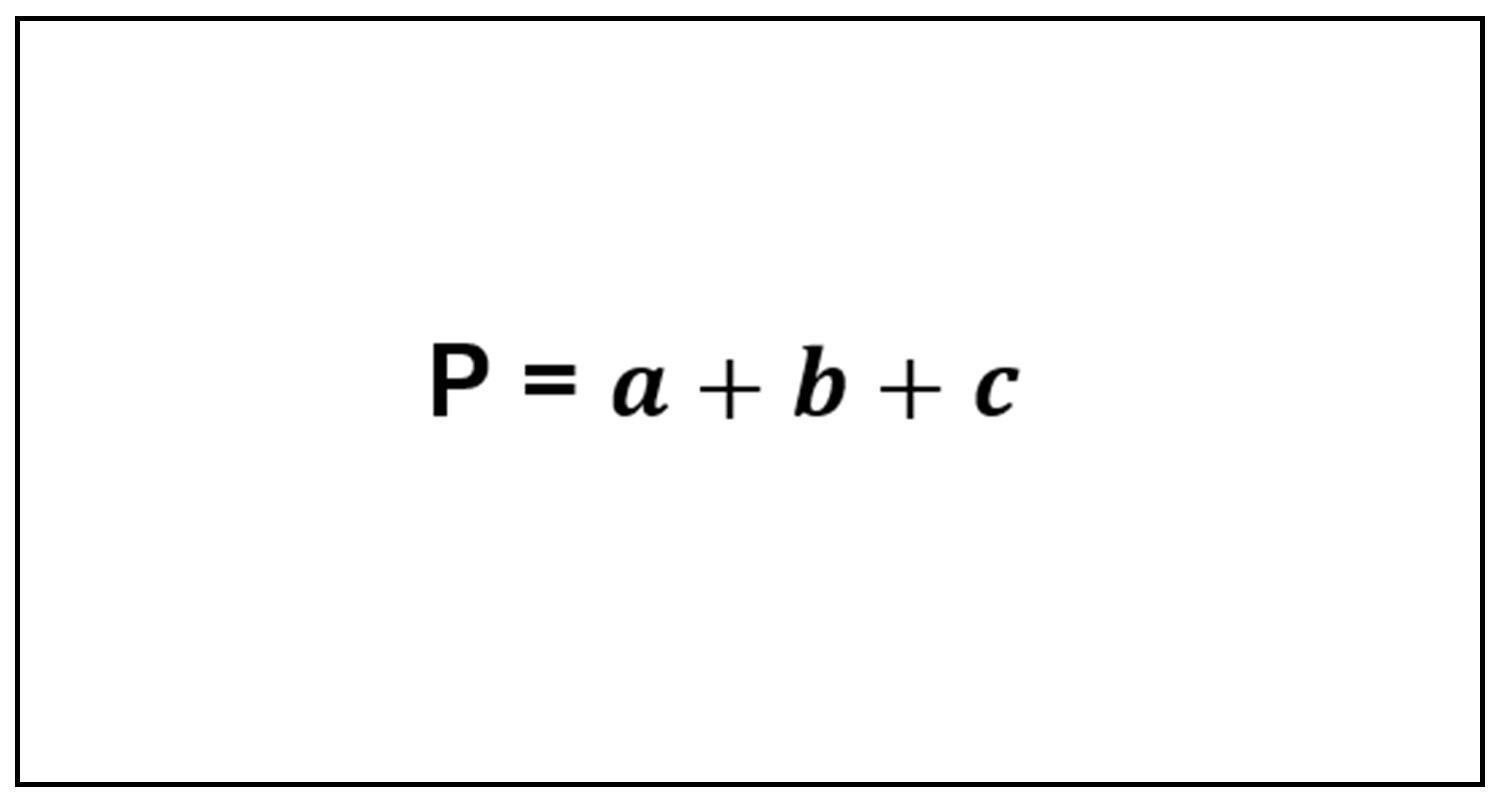
Trong đó:
P: Chu vi tam giác.
a, b, c: Lần lượt 3 cạnh của hình tam giác đó.
Ví dụ: Tính chu vi tam giác ABC khi biết độ dài cạnh AB = 9, AC = 5, BC = 10.
2. Tam giác vuông
Tam giác vuông là tam giác có một góc bằng 90 độ (góc vuông).
– Công thức tính diện tích tam giác vuông
Ví dụ tam giác ABC vuông tại A. Áp dụng công thức tính diện tích tam giác thường để tính, ta có:
Trong đó:
A, B, C: Các đỉnh của tam giác.
a, b, c: Lần lượt kí hiệu cho độ dài các cạnh BC, AC, AB.
ha: Đường cao hạ từ đỉnh A tương ứng.
S: Diện tích của hình tam giác.
Ví dụ: Tính diện tích hình tam giác ABC có độ dài đáy là 32cm và chiều cao là 22cm.
– Công thức tính chu vi tam giác vuông
Tam giác vuông cũng có cách tính chu vi như tam giác thường, bằng tổng độ dài ba cạnh của một tam giác vuông.
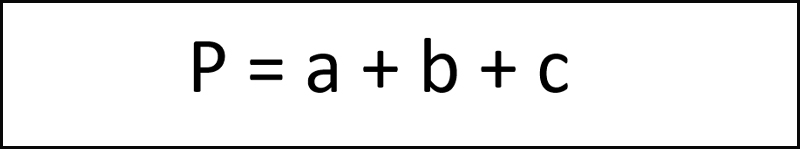
Trong đó:
a, b, c: Lần lượt 3 cạnh của hình tam giác đó.
P: Chu vi tam giác
3. Tam giác cân
Tam giác cân là tam giác có hai cạnh bên bằng nhau và số đo hai góc ở đáy cũng bằng nhau.

– Công thức tính diện tích tam giác cân
Tính diện tích tam giác cân cũng dựa vào đường cao như công thức tính diện tích tam giác thường.
– Công thức tính chu vi tam giác cân
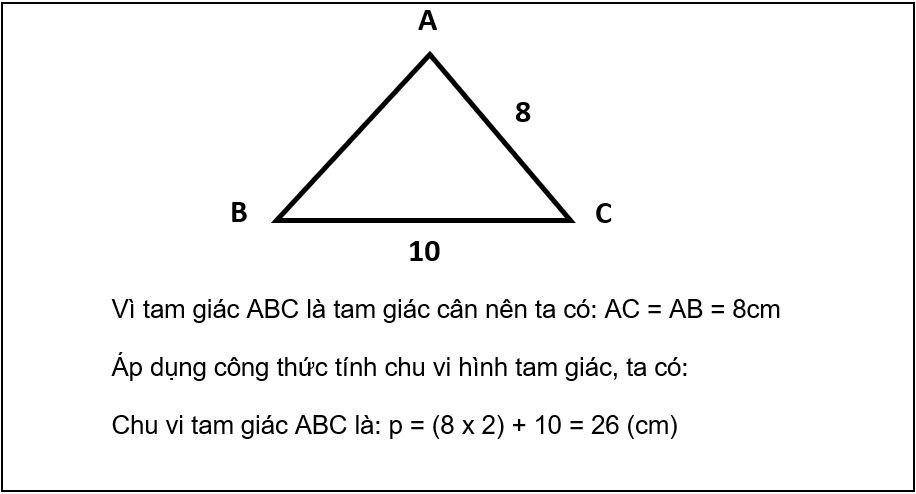
Vì có hai cạnh bên bằng nhau nên công thức tính chu vi tam giác cân được biểu diễn như sau:
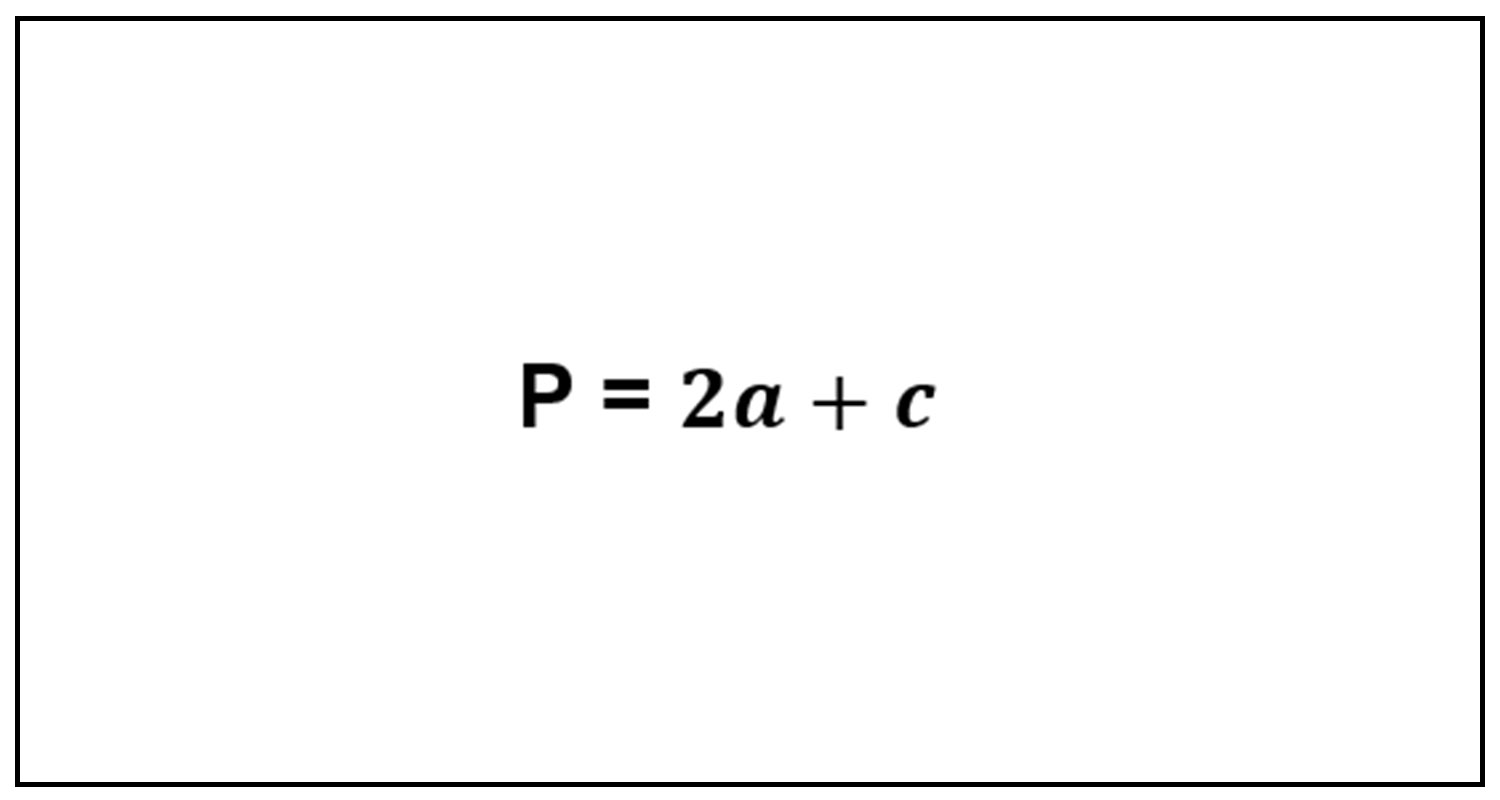
Trong đó:
a: Cạnh bên của tam giác cân.
c: Cạnh đáy của tam giác.
Cùng xem ví dụ dưới đây để hiểu hơn về cách tính chu vi tam giác cân nhé!
Ví dụ: Tính chu vi tam giác cân ABC khi biết chiều dài cạnh bên là 8cm, chiều dài cạnh đáy là 10cm.
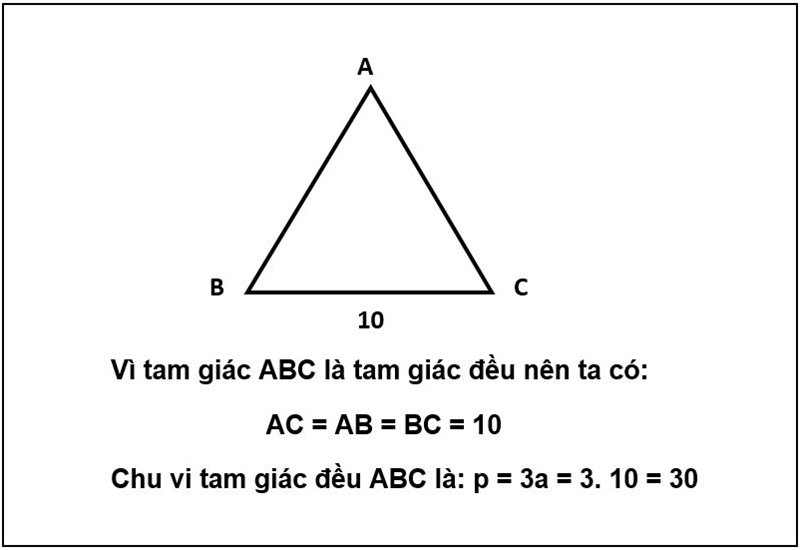
4. Tam giác đều
Tam giác đều là tam giác có độ dài ba cạnh bằng nhau, số đo các góc cũng bằng nhau và bằng 60 độ.
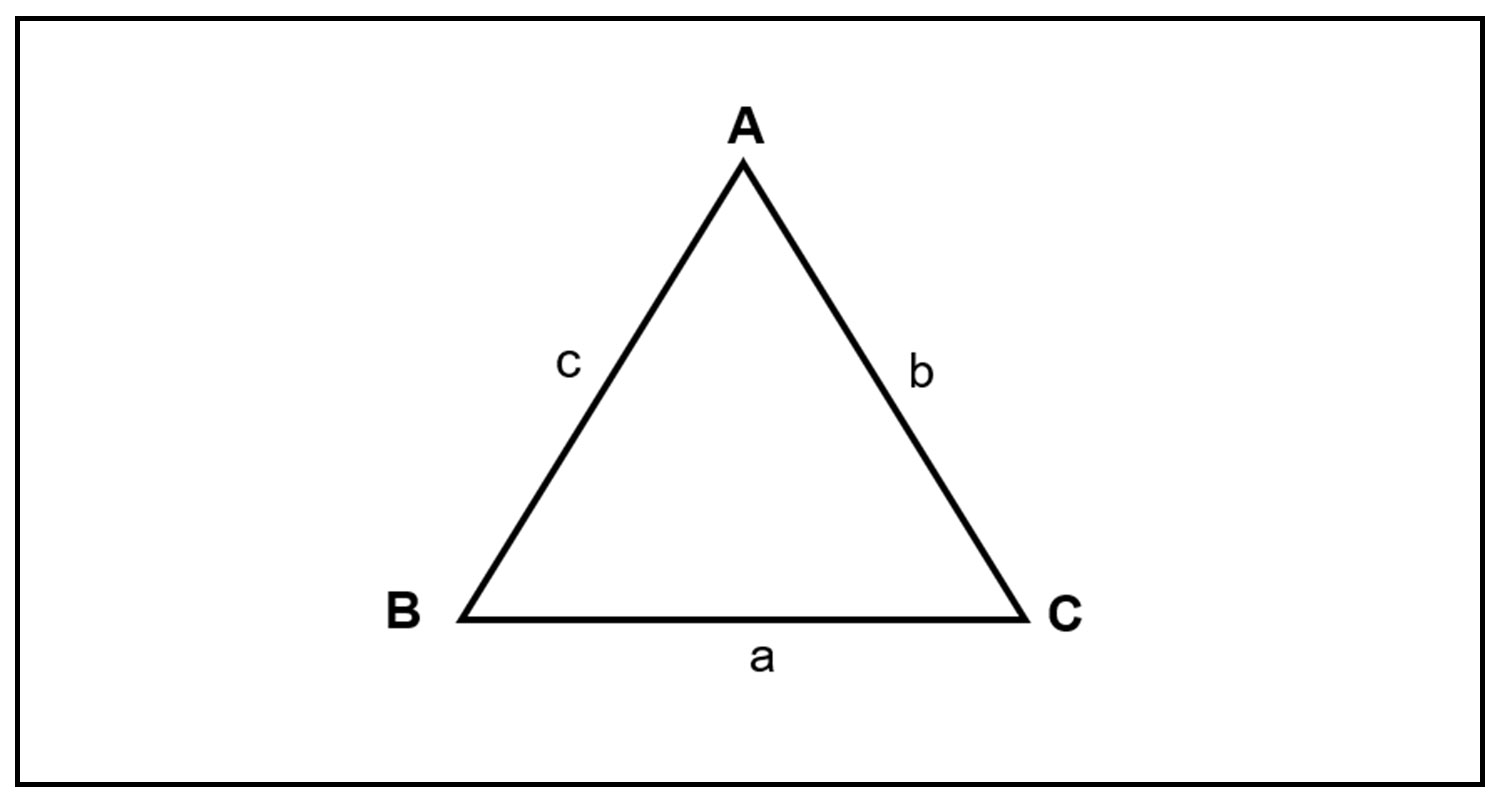
– Công thức tính diện tích tam giác đều
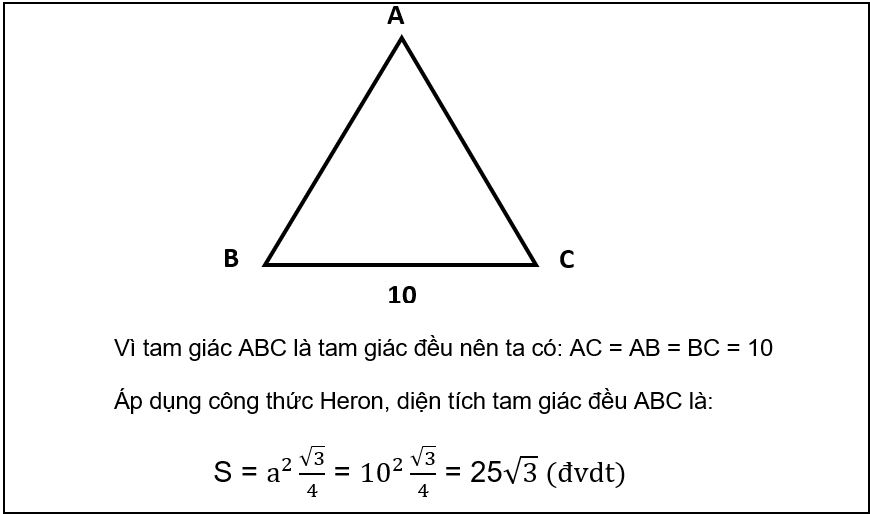
Áp dụng công thức Heron để tính:
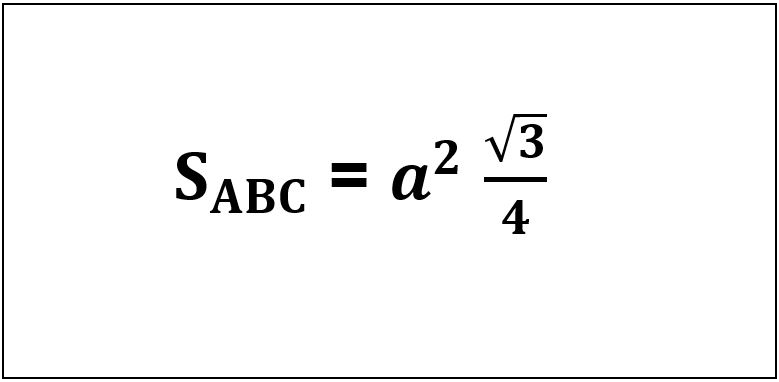
Trong đó:
a: Độ dài các cạnh của tam giác đều.
Ví dụ dưới đây sẽ giúp bạn hiểu hơn về công thức tính diện tích tam giác đều bên trên.
Ví dụ: Tính diện tích tam giác đều ABC, cạnh bằng 10.
– Công thức tính chu vi tam giác đều
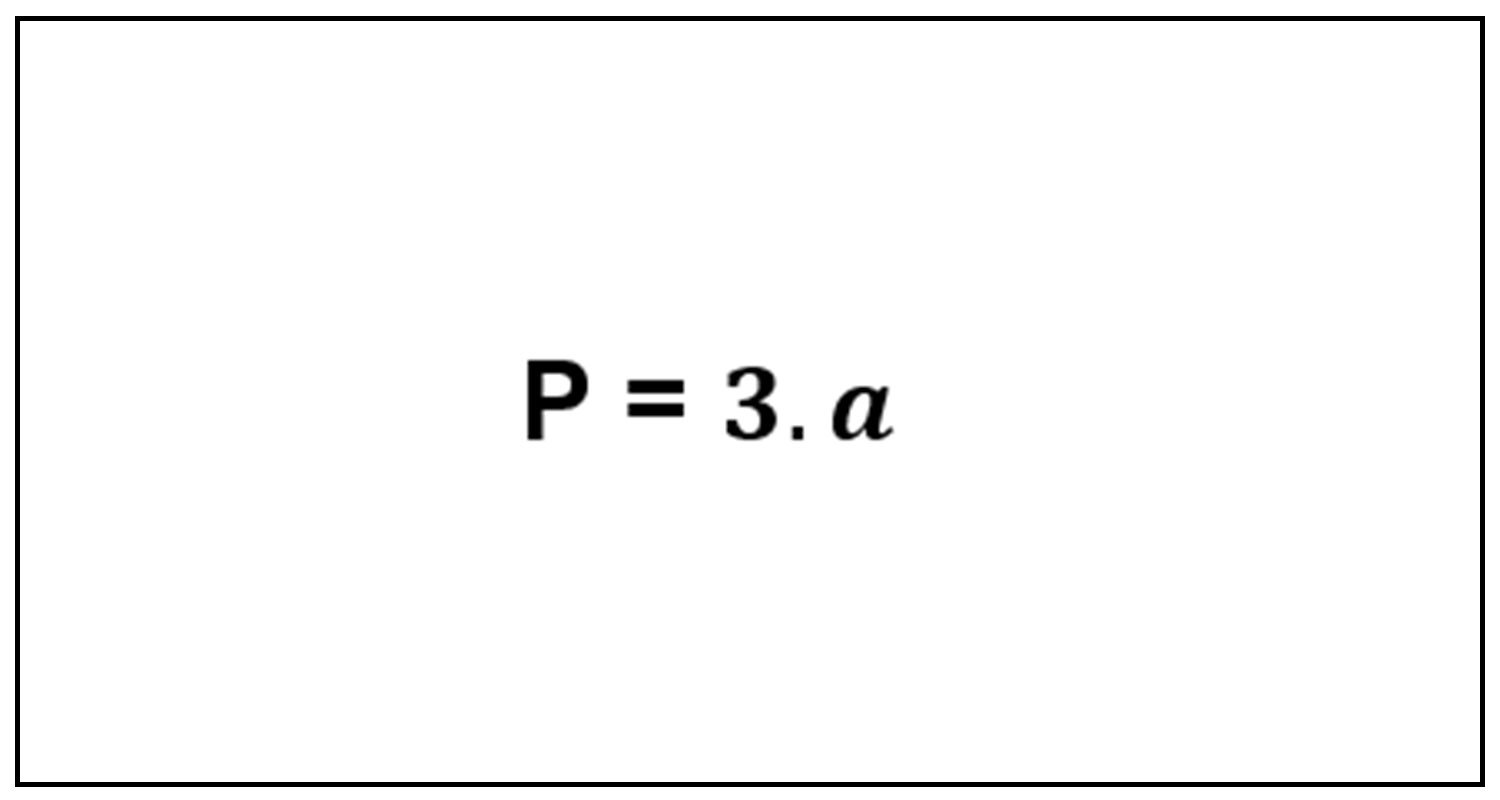
Trong đó:
P: Chu vi tam giác đều.
a: Chiều dài cạnh của tam giác.
Ví dụ: Tính chu vi tam giác đều ABC.
5. Các công thức tính diện tích tam giác trong không gian
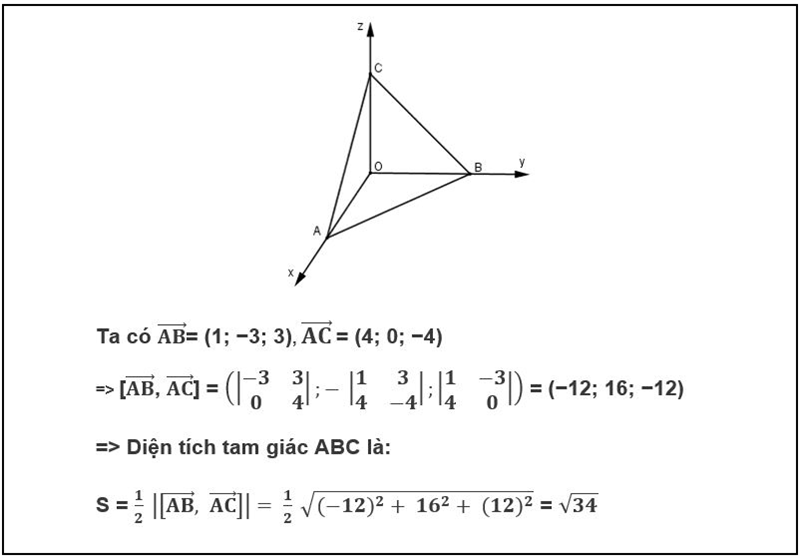
Trong mặt phẳng Oxy, gọi tọa độ các đỉnh của tam giác ABC lần lượt là: A(xA,yA),B(xB,yB),C(xC,yC), ta có thể sử dụng các công thức sau để tính diện tích tam giác

Ví dụ: Trong không gian Oxyz cho 3 điểm A(1;2;1), B(2;-1;3), C(5;2;-3). Tính diện tích của tam giác ABC.
Một số sản phẩm máy tính cầm tay đang kinh doanh tại Thế Giới Di Động
Với các công thức tính trên đây, hy vọng rằng việc tính chu vi, diện tích tam giác vuông, tam giác đều, tam giác cân không còn khó khăn với bạn nữa.