Or you want a quick look: Tính chất ba đường cao của tam giác
Tính chất ba đường cao của tam giác là gì? Đây là một trong những phần lý thuyết khá quan trọng trong môn Toán với các bạn học sinh cấp 2. Trong bài viết này, GiaiNgo sẽ mách nhỏ cho bạn tính chất ba đường cao của tam giác là gì nhé!
Tính chất ba đường cao của tam giác
Tính chất ba đường cao của tam giác là phần kiến thức khá quen thuộc, nằm trong chương trình Toán lớp 7. Tuy nhiên, nhiều bạn học sinh còn gặp khó khăn khi giải các bài tập liên quan đến nó.
Để hiểu rõ hơn về tính chất ba đường cao của tam giác, mời bạn theo dõi bài viết bên dưới của GiaiNgo nhé!
Đường cao của tam giác là gì?
Trước khi tìm hiểu tính chất ba đường cao của tam giác, hãy cùng GiaiNgo ôn lại định nghĩa đường cao của tam giác là gì nhé!
Trong toán học, đường cao của tam giác là đoạn thẳng vuông góc kẻ từ một đỉnh đến đường thẳng và vuông góc với cạnh đối diện. Cạnh đối diện này thường được gọi là đáy tương ứng với đường cao. Mỗi tam giác có ba đường cao.
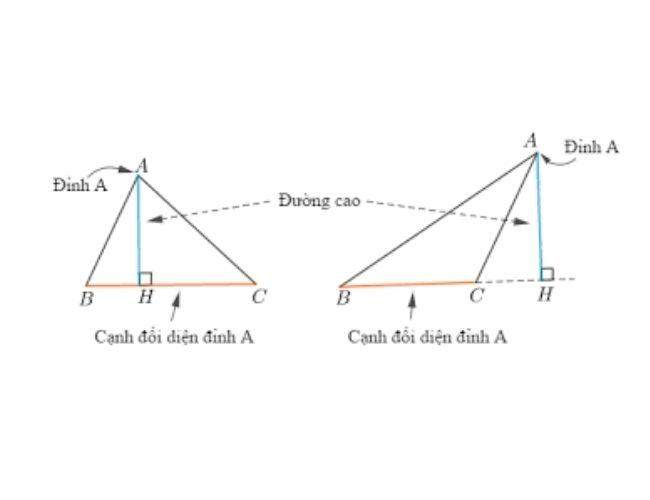
Theo lý thuyết, giao điểm của đường cao với đáy được gọi là chân đường cao. Độ dài của đường cao theo định nghĩa là khoảng cách giữa đỉnh và đáy.
Tính chất ba đường cao của tam giác
Đường cao của tam giác được áp dụng đa dạng các loại bài tập. Vậy bạn có biết tính chất ba đường cao của tam giác là gì không?
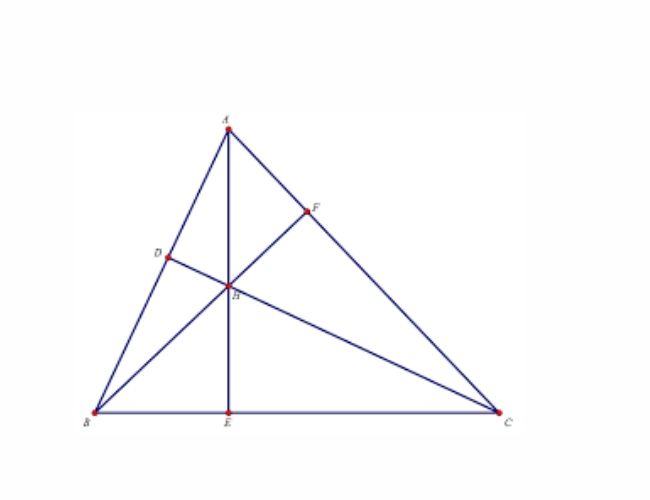
Ba đường cao của một tam giác cùng đi qua một điểm. Điểm đó gọi là trực tâm của tam giác. Một điểm lưu ý nhỏ cho các bạn, trực tâm của một tam giác có thể nằm trong hoặc trùng với một đỉnh hoặc nằm ngoài tam giác đó.
Vẽ đường cao, trung tuyến, trung trực, phân giác của tam giác cân
Tính chất
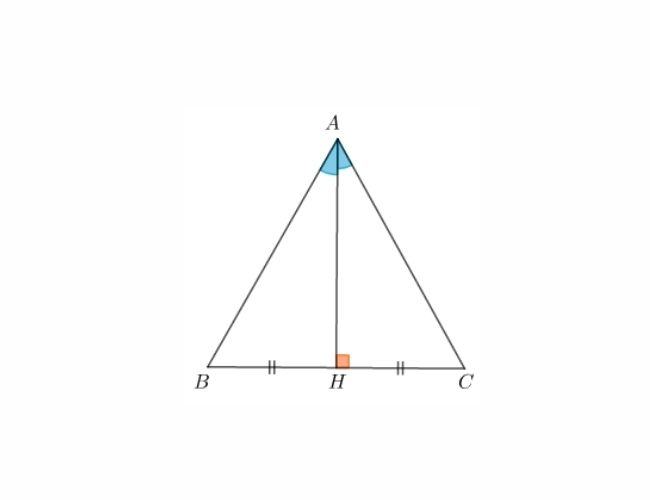
Trong một tam giác cân (tam giác có hai cạnh bằng nhau), đường trung trực ứng với cạnh đáy cũng đồng thời là đường phân giác, đường trung tuyến và đường cao cùng xuất phát từ đỉnh đối diện với cạnh đó.
Giả sử, tam giác cân ABC có AH là đường trung trực. Từ đó, chúng ta có thể suy ra AH là đường phân giác của góc A; AH là đường trung tuyến ứng với cạnh BC; AH là đường cao xuất phát từ đỉnh A.
Nhận xét
Tóm lại để giải tốt các bài tập liên quan đến đường cao, đường trung tuyến, đường trung trực và đường phân giác trong tam giác cân, bạn cần ghi nhớ các tính chất mà GiaiNgo đã gợi ý ở trên. Ngoài ra, bạn cũng có thể áp dụng nhận xét sau đây:
Trong một tam giác, nếu hai trong bốn loại đường (trung tuyến, phân giác và đường cao cùng xuất phát từ một đỉnh và đường trung trực ứng với cạnh đối diện của đỉnh này) trùng nhau thì tam giác đó là tam giác cân.
Tính chất ba đường cao của tam giác đều
Tính chất ba đường cao của tam giác đều là gì? Tiếp tục theo dõi bài viết của GiaiNgo để tìm ra câu trả lời chính xác nhé!
Trong một tam giác đều, trọng tâm, trực tâm, điểm cách đều ba đỉnh, điểm nằm trong tam giác và cách đều ba cạnh là bốn điểm trùng nhau. Giả sử, ta có tam giác ABC và các điểm như hình bên dưới:
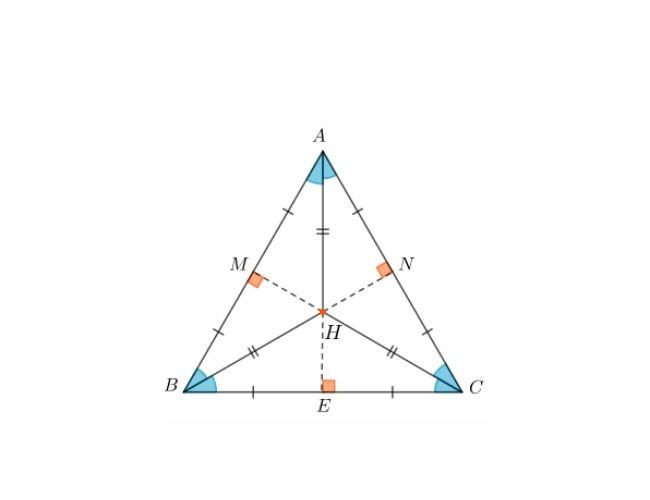
Vì tam giác ABC là tam giác đều nên các bạn có thể suy ra, H là trọng tâm (giao của ba đường trung tuyến); H là trực tâm (giao của ba đường cao); H là điểm cách đều ba đỉnh A, B, C (giao của ba đường trung trực); H là điểm cách đều ba cạnh AB, BC, AC (giao của ba đường phân giác).
Từ đây, có thể thấy đường đặc biệt trong tam giác đều ( đường trung tuyến, đường cao, đường trung trực, đường phân giác) cùng đi qua một điểm.
Câu hỏi, bài tập về tính chất ba đường cao của tam giác
Sau khi kết thúc phần lý thuyết, mời bạn đọc tham khảo một số câu hỏi và bài tập liên quan đến tính chất ba đường cao của tam giác nhé!
Bài 1: Cho ΔABC, hai đường cao AM và BN cắt nhau tại H. Bạn hãy chọn phát biểu đúng:
A. H là trọng tâm của ΔABC
B. H là tâm đường tròn nội tiếp ΔABC
C. CH là đường cao của ΔABC
D. CH là đường trung trực của ΔABC
Đáp án đúng: C. Vì hai đường cao AM và BN cắt nhau tại H nên CH là đường cao của ΔABC và H là trực tâm tam giác ΔABC.
Bài 2: Cho ΔABC cân tại A có AM là đường trung tuyến khi đó:
A. AM ⊥ BC
B. AM là đường trung trực của BC
C. AM là đường phân giác của góc BAC
D. Cả A, B, C đều đúng
Đáp án đúng: D. Vì ΔABC cân tại A có AM là đường trung tuyến nên AM cũng là đường cao, đường trung trực và đường phân giác của tam giác ABC.
Bài tập áp dụng: Cho ΔABC nhọn, hai đường cao BD và CE. Trên tia đối của tia BD lấy điểm I sao cho BI = AC . Trên tia đối của tia CE lấy điểm K sao cho CK = AB. ΔAIK là tam giác gì?
A. ΔAIK là tam giác cân tại B
B. ΔAIK là tam giác vuông cân tại A
C. ΔAIK là tam giác vuông
D. ΔAIK là tam giác đều
Đáp án đúng: B.
Bạn hãy thử áp dụng những kiến thức mà GiaiNgo chia sẻ ở trên để giải bài tập này nhé!
Trên đây là tất tần tật kiến thức về tính chất ba đường cao của tam giác và một số bài tập áp dụng. Theo dõi GiaiNgo để có thêm nhiều kiến thức bổ ích nhé!