Or you want a quick look: Định nghĩa thiết diện là gì?
Thiết diện là một dạng toán khó và thường gặp trong chương trình Toán THPT. Vậy thiết diện là gì? Công thức tính thiết diện Cách xác định thiết diện của hình hộp như nào? Lý thuyết cách xác định thiết diện trong quan hệ song song, vuông góc? Các dạng bài tập về diện tích thiết diện?… Trong nội dung bài viết dưới đây, DINHNGHIA.COM.VN sẽ giúp bạn tổng hợp kiến thức về chủ đề thiết diện là gì, cùng tìm hiểu nhé!
Vuidulich.vn cũng giúp giải đáp những vấn đề sau đây:- Công thức tính thiết diện hình trụ
- Cách xác định thiết diện của hình hộp
- Công thức tính thể tích thiết diện
- Tính diện tích thiết diện lớp 11
- Bài toán tìm thiết diện năng cao
- Công thức tính thiết diện hình vuông
- Công thức tính thiết diện hình nón
- Cách xác định thiết diện trong quan hệ song song
 https://www.youtube.com/watch?v=RitwoibrXPI
https://www.youtube.com/watch?v=RitwoibrXPI
Nội dung chính bài viết
Định nghĩa thiết diện là gì?
Cho hình (mathbb{T}) và mặt phẳng ( (P) ), phần mặt phẳng của ( (P) ) nằm trong (mathbb{T}) được giới hạn bởi các giao tuyến sinh ra do ( (P) ) cắt một số mặt của (mathbb{T}) được gọi là thiết diện.
Theo cách khác, thiết diện được định nghĩa là các đoạn giao tuyến giữa mặt phẳng và hình chóp khi nối nhau sẽ tạo ra một đa giác phẳng. Đó chính là thiết diện (hay còn gọi là mặt cắt) của mặt phẳng với hình chóp đó.
Ví dụ 1: Cho hình chóp ( S.ABCD ). Lấy ( M ) là trung điểm ( SA ). Khi đó mặt phẳng ( (P) ) đi qua ( M ) và song song với mặt phẳng đáy sẽ cắt hình chóp. Thiết diện là tứ giác ( MNPQ ) với ( N,P,Q ) lần lượt là trung điểm ( SB,SC,SD )

Cách xác định thiết diện trong quan hệ song song và vuông góc
Từ định nghĩa thiết diện là gì, chúng ta cùng nhau tìm hiểu về cách xác định thiết diện trong quan hệ song song, vuông góc. Nhìn chung, để tìm thiết diện tạo bởi hình (mathbb{T}) và mặt phẳng ( (P) ) ta làm như sau :
- Bước 1: Tìm giao điểm của mặt phẳng ( (P) ) với các cạnh của hình (mathbb{T}). Ta có thể tìm giao điểm của ( (P) ) với các mặt của hình (mathbb{T}) rồi từ đó xác định các giao điểm với các cạnh.
- Bước 2: Nối các giao điểm tìm được ở trên. Hình đa diện được tạo bởi các đa diện đó chính là thiết diện cần tìm.
Chú ý: Để tìm thiết diện chúng ta sẽ cần sử dụng một số quan hệ song song, vuông góc giữa đường thẳng và mặt phẳng:
- Cho đường thẳng ( d in ( P) ). Mặt phẳng ( (Q) ) song song với ( d ) và cắt ( (P) ) tại giao tuyến là đường thẳng ( d’ ). Khi đó ( d || d’ )
- Cho hai mặt phẳng ( (P),(Q) ) thỏa mãn : (left{begin{matrix} (P) bot (Q) (P) cap (Q ) =d end{matrix}right.). Khi đó nếu (left{begin{matrix} d’ in (P) d’ bot d end{matrix}right. Rightarrow d’ bot (Q))
Cách xác định thiết diện trong quan hệ song song
Bài toán xác định thiết diện song song với đường thẳng.

Ví dụ 2:
Cho hình chóp ( S.ABCD ) có đáy ( ABCD ) là hình bình hành. Gọi ( M ) là một điểm bất kì nằm trên ( SA ). Mặt phẳng ( (P) ) đi qua ( M ) và song song với ( AB ) và ( SC ). Xác định thiết diện của ( S.ABCD ) cắt bởi ( (P) )
Cách giải:

Vì ( (P) || AB ) và ( AB in (SAB) ) nên
(Rightarrow) giao tuyến của ( (P) ) và ( (SAB) ) song song với ( AB )
Trong mặt phẳng ( (SAB) ) dựng ( MN ) song song với ( AB ). Khi đó ((P) cap SB =N)
Ta có:
(left{begin{matrix} (P) || SC SC in (SBC) end{matrix}right. Rightarrow SC || ((P)cap (SBC)))
Như vậy : ((P) cap BC = P) với ( NP || SC )
Tương tự:
(left{begin{matrix} (P) || BC BC in (ABCD) end{matrix}right. Rightarrow SC || ((P)cap (ABCD)))
Như vậy: ((P) cap AD = Q ) với ( PQ || AB )
Vậy ( MNPQ ) là thiết diện cần tìm.
Cách xác định thiết diện trong quan hệ vuông góc
Từ khái niện thiết diện là gì, hãy cùng DINHNGHIA.COM.VN tìm hiểu qua bài toán xác định thiết diện vuông góc với đường thẳng.
Phương pháp:
Cho mặt phẳng (α) cùng với đường thẳng a không vuông góc với (α). Hãy xác định mặt phẳng (β) chứa a và vuông góc với (α).
Cách giải:
- Đầu tiên ta cần chọn một điểm A∈a
- Tiếp theo dựng đường thẳng b đi qua A và vuông góc với (α). Khi đó mp (a,b) chính là mặt phẳng (β).

Ví dụ 3:
Cho hình chóp S.ABCD, có đáy ABCD là hình vuông, bên cạnh đó SA ⊥ (ABCD). Gọi (α) là mặt phẳng chứa AB và vuông góc với (SCD). Vậy (α) cắt chóp S.ABCD theo thiết diện là hình gì?.
Cách giải:

Diện tích thiết diện là gì?
Diện tích thiết diện là gì? Đây hẳn là câu hỏi được rất nhiều học sinh quan tâm. Diện tích thiết diện theo định nghĩa chính là diện tích phần mặt cắt (thiết diện) được tạo bởi mặt phẳng ( (P) ) và hình (mathbb{T}) như đã nói ở trên.
Cách tính thiết diện?
Để tính được diện tích thiết diện thì ta cần sử dụng một số công thức tính diện tích hình phẳng như hình tam giác, hình chữ nhật ,… Sau đó ta có thể chia nhỏ thiết diện thành các hình đơn giản trên để tính toán rồi sau đó cộng lại.
Ví dụ 4:
Cho hình chóp ( S.ABCD ) có đáy là hình vuông tâm ( O ) và ( AB=a ). Biết rằng ( SA bot (ABCD) ) và ( SA = asqrt{2} ). Mặt phẳng ( (P) ) đi qua ( B ) và vuông góc vuoonlt SC [/latex]. Tính diện tích thiết diện của hình chóp ( S.ABCD ) cắt bởi mặt phẳng ( (P) )
Cách giải:

Ta có:
(SA bot (ABCD) Rightarrow SA bot BD)
( BD bot AC ) ( do là hai đường chéo của hình vuông ( ABCD ) )
(Rightarrow BD bot (SAC))
(Rightarrow BD bot SC ;;;; (1))
Trong mặt phẳng ( (SAC) ) kẻ ( OE bot SC ;;;; (2) )
Từ ( (1)(2) Rightarrow (BED) bot SC )
Vậy mặt phẳng ( (BED) ) chính là mặt phẳng ( (P) ) và thiết diện cần tìm là tam giác ( BED )
Vì hình vuông ( ABCD ) có độ dài cạnh ( AB=a ) nên (Rightarrow ) đường chéo ( AC = BD = asqrt{2} ;;;; (3) )
Trong mặt phẳng ( (SAC) ) xét tam giác ( SAC ) vuông tại ( A ).
(Rightarrow SC = sqrt{SA^2+AC^2 }=2a)
(OC = frac{AC}{2} =frac{a}{sqrt{2}})
Xét (Delta SAC) và (Delta OEC) có :
(widehat{A} = widehat{E} =90^{circ})
(widehat{C} ) chung
(Rightarrow Delta SAC sim Delta OEC)
Vậy ta có :
(frac{OE}{SA} = frac{OC}{SC} Rightarrow OE =frac{OC.SA}{SC}=frac{frac{a}{sqrt{2}}.asqrt{2}}{2a}=frac{a}{2} ;;; (4) )
Vì ( BD bot (SAC ) nên ( BD bot EO ;;;; (5) )
Từ ( (3)(4)(5) ) ta có :
(S_{BED}=frac{BD.EO}{2}=frac{asqrt{2}.frac{a}{2}}{2}=frac{a^2}{2sqrt{2}})
Vậy diện tích thiết diện là (frac{a^2}{2sqrt{2}}) đơn vị diện tích
Công thức tính thiết diện của một số hình đặc biệt
Các ví dụ trên chúng ta đã cùng nói về khái niệm thiết diện là gì, kiến thức thiết diện của hình chóp. Bây giờ chúng ta sẽ nói đến thiết diện của một số hình khối khác.
Cách xác định thiết diện của hình trụ
Định nghĩa hình trụ là gì?
Khi quay một hình chữ nhật quanh một trục cố định, ta được một hình trụ với hai đáy là hai đường tròn bằng nhau.
Ví dụ thiết diện hình trụ

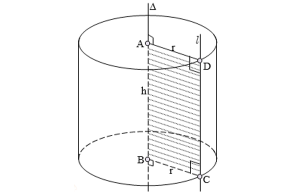
- Nếu cắt mặt trụ tròn xoay (có bán kính là ( r ) ) bởi một mặt phẳng ( (alpha ) ) vuông góc với trục ( Delta ) ( song song với hai mặt đáy ) thì ta được thiết diện là đường tròn có tâm nằm trên ( Delta ) và có bán kính bằng ( r )
- Nếu cắt mặt trụ tròn xoay (có bán kính là ( r ) ) bởi một mặt phẳng ( (alpha ) ) không vuông góc với trục ( Delta ) nhưng cắt tất cả các đường sinh thì ta được thiết diện là một đường Elip có trục nhỏ bằng ( 2r ) và trục lớn bằng (frac{2r}{sin phi}) với (phi) là góc giữa trục ( Delta ) và mặt phẳng ( ( alpha ) ) và (0 < phi< 90^{circ})
Cho mặt phẳng ( ( alpha ) ) song song với trục ( Delta ) của mặt trụ tròn xoay và cách ( Delta ) một khoảng ( k ) .
- Nếu ( k<r ) thì mặt phẳng ( ( alpha ) ) cắt mặt trụ theo hai đường sinh và thiết diện là hình chữ nhật.
- Nếu ( k=r ) thì mặt phẳng ( ( alpha ) ) tiếp xúc với mặt trụ theo một đường sinh.
- Nếu ( k >r ) thì mặt phẳng ( ( alpha ) ) không cắt mặt trụ.

Ví dụ 5:
Một hình trụ có bán kính đáy bằng ( 3a ) và thể tích bằng ( 90pi a^3 ). Một mặt phẳng song song với trục và cách trục ( 2a ) cắt khối chóp tạo thành một thiết diện. Tính diện tích thiết diện đó
Cách giải:

Do mặt phẳng song song với trục và cách trục ( 2a < 3a=r ) nên (Rightarrow) thiết diện là hình chữ nhật ( ABCD ) với ( AB=CD ) là đường cao của hình trụ
Do đó : (AB=CD = frac{V}{S}=frac{90pi a^3}{2pi. 9a^2}=5a)
Kẻ ( OH bot BC ). Do tam giác ( OBC ) cân tại ( O ) nên ta có :
(left{begin{matrix} OH = 2a OB = 3a end{matrix}right.Rightarrow BC =2BH = 2sqrt{OB^2-OH^2}=2sqrt{5}a)
Như vậy diện tích thiết diện :
(S_{ABCD}=AB.BC= 5a. 2sqrt{5}a=10sqrt{5}a^2) đơn vị diện tích
Cách xác định thiết diện của hình hộp
Hình hộp là hình lăng trụ có đáy là hình bình hành.
Hình hộp có ( 6 ) mặt là hình bình hành. Hai mặt đối diện song song và bằng nhau
Hình hộp có ( 12 ) cạnh chia làm ( 3 ) nhóm. Mỗi nhóm gồm ( 4 ) cạnh song song và bằng nhau.

Để xác định thiết diện của hình hộp khi cắt bởi mặt phẳng ( (alpha) ) thì ta cần sử dụng các quan hệ song song, vuông góc để tìm giao của ( (alpha) ) với các cạnh của hình hộp.
Ví dụ 6:
Cho hình hộp ( ABCD.A’B’C’D’ ). Trên ba cạnh ( AB, DD’,BB’ ) lần lượt lấy ba điêm ( M,N,P ) thỏa mãn (frac{AM}{AB}=frac{D’N}{D’D}=frac{B’P}{B’B})
Xác định thiết diện của hình hộp khi cắt bởi mặt phẳng ( (MNP) )
Cách giải:

Trên ( AD ) lấy điểm ( E ) sao cho : (frac{AM}{AB}=frac{AE}{AD})
(Rightarrow ME || BD)
Vì (frac{B’P}{B’B}=frac{D’N}{D’D}Rightarrow PN || B’D’Rightarrow PN || BD)
(Rightarrow ME || PN Rightarrow E in (MNP) ;;;; (1))
Trên ( B’C’ ) lấy điểm ( F ) sao cho : (frac{B’F}{B’C}=frac{B’P}{B’B})
(Rightarrow PF || BC’)
Vì (frac{AE}{AD}=frac{D’N}{D’D}Rightarrow EN || AD’Rightarrow EN || BC’)
(Rightarrow PF || EN Rightarrow F in (MNP) ;;;; (2))
Trên ( C’D’ ) lấy điểm ( K ) sao cho : (frac{C’K}{C’D’}=frac{C’F}{C’B’})
(Rightarrow KF || B’D’)
Vì ( PN || B’D’ Rightarrow PN || KF Rightarrow K in (MNP) ;;;; (3))
Từ ( (1)(2)(3) Rightarrow ) thiết diện là lục giác ( MPFKNE )
Cách tìm thiết diện của hình lập phương
Hình lập phương là một hình hộp đặc biệt, do đó các tìm thiết diện khi cắt hình lập phương bởi mặt phẳng ( (alpha) ) cũng giống như bài toán tìm thiết diện của hình hộp chữ nhật. Tuy nhiên do tính chất đặc biệt của hình lập phương mà chúng ta có thể sử dụng các tính chất đó để tìm thiết diện một cách dễ dàng hơn
Ví dụ 7:
Cho hình lập phương ( ABCD.A’B’C’D’ ) có độ dài cạnh bằng ( a ) . Gọi ( M,N,P ) lần lươt là trung điểm ( AD, CD, BB’ ). Tính diện tích thiết diện của hình lập phương bị cắt bởi mặt phẳng ( (MNP) )
Cách giải:

Xét mặt phẳng ( (ABCD) ). Kéo dài ( MN ) cắt đường thẳng ( AB,BC ) lần lượt tại ( K,H )
Gọi (left{begin{matrix} F= PK cap AA’ E= PH cap CC’ end{matrix}right.)
Như vậy thiết diện cần tìm là ngũ giác ( MNEPF )
Ta có :
(left{begin{matrix} MN ||AC AM || CH end{matrix}right. Rightarrow AMHC) là hình bình hành
(Rightarrow CH = AM =frac{a}{2})
Tương tự ta được : (Rightarrow AK=CH =frac{a}{2})
(Rightarrow BK=BH =frac{3a}{2})
Theo định lý Pitago (Rightarrow PH=PK =sqrt{BP^2+BK^2}=frac{asqrt{10}}{2})
Do ( AF|| BP ) nên (frac{PF}{PK}=frac{BA}{BK}Rightarrow PF =frac{BA.PK}{BK}=frac{a.frac{asqrt{10}}{2}}{frac{3a}{2}}=frac{asqrt{10}}{3})
Tương tự ta cũng có (PE=frac{asqrt{10}}{3})
Mặt khác (frac{AF}{BP}=frac{KA}{KB}=frac{HC}{HB}=frac{CE}{BP} Rightarrow AF = CE Rightarrow ACEF) là hình bình hành
(Rightarrow EF=AC =asqrt{2})
Như vậy tam giác ( PEF ) cân tại ( P ) và có :
(left{begin{matrix} PE=PF =frac{asqrt{10}}{3} EF= AC =asqrt{2} end{matrix}right.)
Vậy (S_{PEF}= frac{EF.2sqrt{PF^2-(frac{EF}{2})^2}}{2}=asqrt{2}.sqrt{frac{10a^2}{9}-frac{a^2}{2}}= frac{a^2sqrt{11}}{3} ;;;; (1) )
Do (Delta AMF = Delta CNE) (c.g.c) nên
(Rightarrow MF=EN)
Mặt khác (Rightarrow MN ||EF) ( do cùng song song với ( AC ) )
(Rightarrow MNEF) là hình thang cân có (left{begin{matrix} MN =frac{a}{2} EF= asqrt{2} end{matrix}right.)
Kẻ ( MI bot EF ), ta có :
(FI=frac{EF-MN}{2}=frac{2sqrt{2}-1}{4}a)
(frac{AF}{BP}=frac{KA}{KB} Rightarrow AF = frac{KA.BP}{KB} = frac{a}{3})
(Rightarrow FM =sqrt{AF^2+AM^2}=frac{asqrt{13}}{6})
Như vậy (Rightarrow MI = sqrt{FM^2-FI^2}=frac{asqrt{36sqrt{2}-29}}{12})
(Rightarrow S{MNEF}=frac{(MN+EF).MI}{2}=frac{(2sqrt{2}+1)sqrt{36sqrt{2}-29}}{24}a^2 ;;;; (2))
Từ ((1)(2) Rightarrow S{MNEPF}=S_{PEF}+S_{MNEF}=frac{8sqrt{11}+(2sqrt{2}+1)sqrt{36sqrt{2}-29}}{24}a^2) đon vị diện tích
Cách xác định thiết diện của hình trụ cực hay
Bài giảng: Tất tần tật về Mặt trụ - Cô Nguyễn Phương Anh (Giáo viên VietJack)A. Phương pháp giải & Ví dụ
- Nếu cắt mặt trụ tròn xoay (có bán kính là r) bởi một mặt phẳng (α) vuông góc với trục Δ thì ta được đường tròn có tâm trên Δ và có bán kính bằng r với r cũng chính là bán kính của mặt trụ đó. - Nếu cắt mặt trụ tròn xoay (có bán kính là r) bởi một mặt phẳng (α) không vuông góc với trục Δ nhưng cắt tất cả các đường sinh, ta được giao tuyến là một đường elíp có trụ nhỏ bằng 2r và trục lớn bằng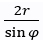 , trong đó φ là góc giữa trục Δ và mặt phẳng (α) với 0 < φ < 90º.
- Cho mặt phẳng (α) song song với trục Δ của mặt trụ tròn xoay và cách Δ một khoảng k.
+ Nếu k < r thì mặt phẳng (α) cắt mặt trụ theo hai đường sinh thì thiết diện là hình chữ nhật.
+ Nếu k = r thì mặt phẳng (α) tiếp xúc với mặt trụ theo một đường sinh.
+ Nếu k > r thì mặt phẳng (α) không cắt mặt trụ.
, trong đó φ là góc giữa trục Δ và mặt phẳng (α) với 0 < φ < 90º.
- Cho mặt phẳng (α) song song với trục Δ của mặt trụ tròn xoay và cách Δ một khoảng k.
+ Nếu k < r thì mặt phẳng (α) cắt mặt trụ theo hai đường sinh thì thiết diện là hình chữ nhật.
+ Nếu k = r thì mặt phẳng (α) tiếp xúc với mặt trụ theo một đường sinh.
+ Nếu k > r thì mặt phẳng (α) không cắt mặt trụ.
Ví dụ minh họa
Bài 1: Khối trụ có thiết diện qua trục là hình vuông cạnh 2a, tính diện tích xung quanh, diện tích toàn phần và thể tích của khối trụ Hướng dẫn: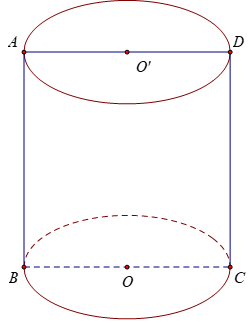 Thiết diện là hình vuông ABCD cạnh 2a
Đường cao của hình trụ là AB = 2a, bán kính đáy OB = a.
Diện tích xung quanh của khối trụ là: Sxq = 2πrh=2π.a.2a=4πa2
Diện tích toàn phần của khối trụ là Stp = 2πrh+2πr2=4πa2+2πa2=6πa2
Thể tích của khối trụ là: V=πr2 h=π.a2.2a=2πa3
Bài 2: Khối trụ có bán kính đáy R = a .Thiết diện song song với trục và cách trục khối trụ một khoảng bằng a/2 là hình chữ nhật có diện tích bằng a2 √3 .Tính thể tích khối trụ
Hướng dẫn:
Thiết diện là hình vuông ABCD cạnh 2a
Đường cao của hình trụ là AB = 2a, bán kính đáy OB = a.
Diện tích xung quanh của khối trụ là: Sxq = 2πrh=2π.a.2a=4πa2
Diện tích toàn phần của khối trụ là Stp = 2πrh+2πr2=4πa2+2πa2=6πa2
Thể tích của khối trụ là: V=πr2 h=π.a2.2a=2πa3
Bài 2: Khối trụ có bán kính đáy R = a .Thiết diện song song với trục và cách trục khối trụ một khoảng bằng a/2 là hình chữ nhật có diện tích bằng a2 √3 .Tính thể tích khối trụ
Hướng dẫn:
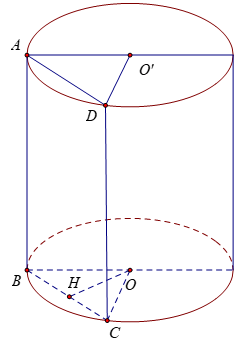 ∆BOC cân tại O có OH là đường cao
⇒ H là trung điểm của BC
∆BOC cân tại O có OH là đường cao
⇒ H là trung điểm của BC
 ABCD là hình chữ nhật nên:
SABCD = AB.BC=AB.a√3=a2 √3⇒ AB=a
Thể tích của khối trụ là:
V=πr2 h=π.a2.a= πa3
Bài 3: Cắt khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật ABCD có AB và CD thuộc hai đáy của khối trụ. Biết AD = 12 cm và góc ACD bằng 60º. Tính thể tích của khối trụ
Hướng dẫn:
ABCD là hình chữ nhật nên:
SABCD = AB.BC=AB.a√3=a2 √3⇒ AB=a
Thể tích của khối trụ là:
V=πr2 h=π.a2.a= πa3
Bài 3: Cắt khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật ABCD có AB và CD thuộc hai đáy của khối trụ. Biết AD = 12 cm và góc ACD bằng 60º. Tính thể tích của khối trụ
Hướng dẫn:
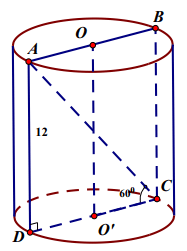 Xét tam giác ADC vuông tại C có:
Xét tam giác ADC vuông tại C có:
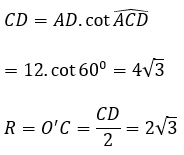 Thể tích của khối trụ là:
V=πr2 h=π.(2√3)2.12=144π
Bài 4: Một hình trụ có bán kính đáy r = 5a và khoảng cách giữa hai đáy bằng 7a. Cắt khối trụ bởi một mặt phẳng song song với trục và cách trục 3a. Tính diện tích của thiết diện.
Hướng dẫn:
Thể tích của khối trụ là:
V=πr2 h=π.(2√3)2.12=144π
Bài 4: Một hình trụ có bán kính đáy r = 5a và khoảng cách giữa hai đáy bằng 7a. Cắt khối trụ bởi một mặt phẳng song song với trục và cách trục 3a. Tính diện tích của thiết diện.
Hướng dẫn:
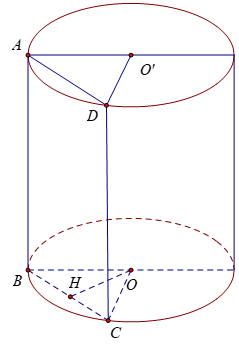 Thiết diện tạo thành là hình chữ nhật ABCD có AB = 7a
Từ O kẻ OH vuông góc với BC
⇒ OH=3a
∆BOC cân tại O có OH là đường cao
⇒ H là trung điểm của BC
Thiết diện tạo thành là hình chữ nhật ABCD có AB = 7a
Từ O kẻ OH vuông góc với BC
⇒ OH=3a
∆BOC cân tại O có OH là đường cao
⇒ H là trung điểm của BC
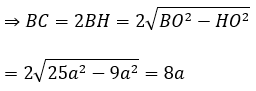 Diện tích của thiết diện là:
SABCD = AB.BC=7a.8a = 56a2
Bài 5: Một hình trụ có diện tích xung quanh là 4π, thiết diện qua trục là một hình vuông. Một mp (P) song song với trục, cắt hình trụ theo thiết diện ABB’A’, biết một cạnh của thiết diện là một dây của đường tròn đáy hình trụ và căng một cung 120º. Tính diện tích thiết diện ABB’A’ .
Hướng dẫn:
Diện tích của thiết diện là:
SABCD = AB.BC=7a.8a = 56a2
Bài 5: Một hình trụ có diện tích xung quanh là 4π, thiết diện qua trục là một hình vuông. Một mp (P) song song với trục, cắt hình trụ theo thiết diện ABB’A’, biết một cạnh của thiết diện là một dây của đường tròn đáy hình trụ và căng một cung 120º. Tính diện tích thiết diện ABB’A’ .
Hướng dẫn:
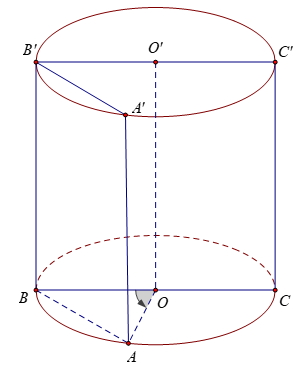 Gọi h, r là chiều cao và bán kính đáy của trụ.
Thiết diện qua trục là hình vuông BCC’B’ cạnh a
Gọi h, r là chiều cao và bán kính đáy của trụ.
Thiết diện qua trục là hình vuông BCC’B’ cạnh a
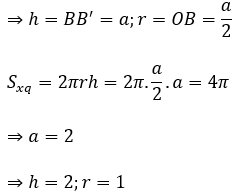 Dây AB căng cung 120º nên ∠(BOA) = 120º
Xét tam giác BOA có :
Dây AB căng cung 120º nên ∠(BOA) = 120º
Xét tam giác BOA có :
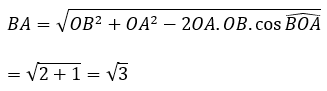 Diện tích thiết diện BAA’B’ là :
S=AB.BB'=2√3
Diện tích thiết diện BAA’B’ là :
S=AB.BB'=2√3
B. Bài tập vận dụng
Bài 1: Một khối trụ có bán kính đáy bằng r và có thiết diện qua trục là một hình vuông. Gọi V là thể tích hình lăng trụ tứ giác đều nội tiếp trong hình trụ và V' là thể tích khối trụ. Hãy tính tỉ số V/V'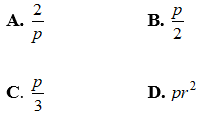 Bài 2: Cho hình trụ có thiết diện qua trục là hình vuông ABCD cạnh 2√3cm với AB là đường kính của đường tròn đáy tâm O. Gọi M là điểm thuộc AB sao cho ∠ ABM = 60º. Thể tích của khối tứ diện ACDM. bằng:
Bài 2: Cho hình trụ có thiết diện qua trục là hình vuông ABCD cạnh 2√3cm với AB là đường kính của đường tròn đáy tâm O. Gọi M là điểm thuộc AB sao cho ∠ ABM = 60º. Thể tích của khối tứ diện ACDM. bằng:
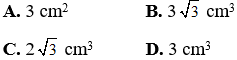 Bài 3: Một hình trụ (T) có diện tích xung quanh bằng 4π và thiết diện qua trục của hình trụ này là một hình vuông. Diện tích toàn phần của (T) là :
Bài 3: Một hình trụ (T) có diện tích xung quanh bằng 4π và thiết diện qua trục của hình trụ này là một hình vuông. Diện tích toàn phần của (T) là :
 Bài 4: Cho một hình trụ (H) có trục ∆. Một mặt phẳng (P) song song với trục ∆ và cách trục ∆ một khoảng k. Nếu k > r thì kết luận nào sau đây là đúng:
A. Mp (P) tiếp xúc với mặt trụ theo một đường sinh.
B. Mp (P) cắt mặt trụ theo hai đường sinh.
C. Mp (P) cắt mặt trụ theo một đường sinh.
D. Mp (P) không cắt mặt trụ.
Bài 5: Khối trụ (T) có bán kính đáy là R và thiết diện qua trục là một hình vuông. Thể tích của khối lăng trụ tứ giác đều nội tiếp khối trụ (T) trên tính theo R bằng:
Bài 4: Cho một hình trụ (H) có trục ∆. Một mặt phẳng (P) song song với trục ∆ và cách trục ∆ một khoảng k. Nếu k > r thì kết luận nào sau đây là đúng:
A. Mp (P) tiếp xúc với mặt trụ theo một đường sinh.
B. Mp (P) cắt mặt trụ theo hai đường sinh.
C. Mp (P) cắt mặt trụ theo một đường sinh.
D. Mp (P) không cắt mặt trụ.
Bài 5: Khối trụ (T) có bán kính đáy là R và thiết diện qua trục là một hình vuông. Thể tích của khối lăng trụ tứ giác đều nội tiếp khối trụ (T) trên tính theo R bằng:
 Bài 6: Cắt hình trụ (T) bằng một mặt phẳng đi qua trục được thiết diện là một hình chữ nhật có diện tích bằng 30cm2 và chu vi bằng 26cm. Biết chiều dài của hình chữ nhật lớn hơn đường kính mặt đáy của hình trụ (T). Diện tích toàn phần của (T) là:
Bài 6: Cắt hình trụ (T) bằng một mặt phẳng đi qua trục được thiết diện là một hình chữ nhật có diện tích bằng 30cm2 và chu vi bằng 26cm. Biết chiều dài của hình chữ nhật lớn hơn đường kính mặt đáy của hình trụ (T). Diện tích toàn phần của (T) là:
 Bài 7: Cắt hình trụ (T) bằng một mặt phẳng song song với trục và cách trục một khoảng bằng 2cm được thiết diện là một hình vuông có diện tích bằng 16cm2. Thể tích của (T) là:
Bài 7: Cắt hình trụ (T) bằng một mặt phẳng song song với trục và cách trục một khoảng bằng 2cm được thiết diện là một hình vuông có diện tích bằng 16cm2. Thể tích của (T) là:
 Bài 8: Một hình trụ có đường cao bằng bán kính đáy bằng 5. Mặt phẳng (P) song song với trục của hình trụ và cắt hình trụ theo thiết diện là hình vuông. Khoảng cách từ trục hình trụ đến mặt phẳng (P) là:
Bài 8: Một hình trụ có đường cao bằng bán kính đáy bằng 5. Mặt phẳng (P) song song với trục của hình trụ và cắt hình trụ theo thiết diện là hình vuông. Khoảng cách từ trục hình trụ đến mặt phẳng (P) là:
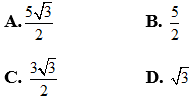 Bài 9: Khối trụ có thiết diện qua trục là một hình vuông cạnh bằng a. Mệnh đề nào dưới đây là mệnh đề sai:
Bài 9: Khối trụ có thiết diện qua trục là một hình vuông cạnh bằng a. Mệnh đề nào dưới đây là mệnh đề sai:
 Bài 10: Cho hình trụ có trục O1 O2. Một mặt phẳng (α) song song với trục O1 O2, cắt hình trụ theo thiết diện là hình chữ nhật ABCD. Gọi O là tâm của thiết diện đó, bán kính đường tròn ngoại tiếp hình chữ nhật ABCD bằng bán kính đường tròn đáy hình trụ. Góc ∠(O1 OO2) bằng
Bài 10: Cho hình trụ có trục O1 O2. Một mặt phẳng (α) song song với trục O1 O2, cắt hình trụ theo thiết diện là hình chữ nhật ABCD. Gọi O là tâm của thiết diện đó, bán kính đường tròn ngoại tiếp hình chữ nhật ABCD bằng bán kính đường tròn đáy hình trụ. Góc ∠(O1 OO2) bằng

Một số dạng bài tập về diện tích thiết diện
Sau đây là một số bài tập tìm thiết diện và diện tích thiết diện có đáp số để các bạn có thể tự luyện tập.
Bài 1:
Cho hình chóp tứ giác đều ( S.ABCD ) có độ dài cạnh đáy bằng ( a ). Gọi ( M,N,P ) lần lượt là trung điểm của ( SA,SB,SC ). Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng ( (MNP) ) và tính diện tích thiết diện đó ?
Đáp số : Thiết diện là ( MNPQ ) với ( Q ) là trung điểm ( SD ) và (S_{MNPQ}=frac{a^2}{4})
Bài 2 :
Cho tứ diện ( ABCD ) có ( AB bot CD ) và ( AB=a; CD =b ). Gọi ( I,J ) lần lượt là trung điểm ( AB, CD ). Trên ( IJ ) lấy điểm ( M ) sao cho (IM = frac{IJ}{3}). Mặt phẳng ( (alpha) ) đi qua ( M ) và song song với ( AB,CD ) cắt tứ diện tạo thành một thiết diện. Tính diện tích thiết diện đó ?
Đáp số : (S= frac{2ab}{9})
Bài 3:
Cho hình trụ tròn xoay có trục là ( OO’ ). Thiết diện qua trục ( OO’ ) là một hình vuông cạnh bằng ( 2a ). Gọi ( M ) là trung điểm ( OO’ ). Mặt phẳng ( (P) ) đi qua ( M ) tạo với đáy một góc bằng (30 ^{circ}) cắt khối trụ theo một thiết diện hình Elip. Tính diện tích thiết diện Elip đó ?
Đáp số : (S= frac{2pi}{sqrt{3}}a^2)
Bài viết trên đây của DINHNGHIA.COM.VN đã giúp bạn tổng hợp lý thuyết thiết diện là gì, cách tìm thiết diện cũng như công thức tính diện tích thiết diện. Hy vọng kiến thức trong bài viết sẽ giúp ích cho bạn trong quá trình học tập và nghiên cứu về chủ đề thiết diện là gì. Chúc bạn luôn học tốt!
Xem chi tiết qua bài giảng của thầy Nguyễn Quốc Chí:(Nguồn: www.youtube.com)
Xem thêm:
Vuidulich.vn cũng giúp giải đáp những vấn đề sau đây:- Công thức tính thiết diện hình trụ
- Cách xác định thiết diện của hình hộp
- Công thức tính thể tích thiết diện
- Tính diện tích thiết diện lớp 11
- Bài toán tìm thiết diện năng cao
- Công thức tính thiết diện hình vuông
- Công thức tính thiết diện hình nón
- Cách xác định thiết diện trong quan hệ song song