Thể tích khối chóp là gì? Công thức tính thể tích khối chóp như thế nào? Mời các bạn hãy cùng Mobitool theo dõi bài viết dưới đây nhé.
Tài liệu Thể tích khối chóp tổng hợp toàn bộ kiến thức như hình chóp là gì, cách tích thể tích hình chóp, các dạng bài tập và ví dụ kèm theo. Thông qua tài liệu này các bạn lớp 12 có thêm nhiều tư liệu tham khảo, trau dồi kiến thức để giải nhanh các bài tập về thể tích khối chóp.
I. Hình chóp là gì?
Hình chóp là hình có mặt đáy là một đa giác và các mặt bên là những tam giác có chung một đỉnh. Đỉnh này được gọi là đỉnh của hình chóp. Đường cao của hình chóp là đường thẳng đi qua đỉnh và vuông góc với mặt phẳng đáy.
Tên gọi của hình chóp dựa vào đa giác đáy: hình chóp tam giác có đáy là tam giác, hình chóp tứ giác có đáy là tứ giác.
II. Công thức thể tích khối chóp
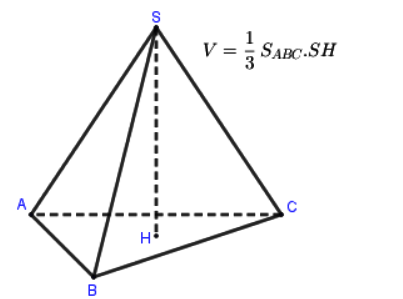
– Công thức thể tích khối chóp
Trong đó: S là diện tích đáy, h là chiều cao khối chóp.
– Một phép vị tự tỉ số k biến khối đa diện có thể tích V thành khối đa diện thể tích V’ thì:
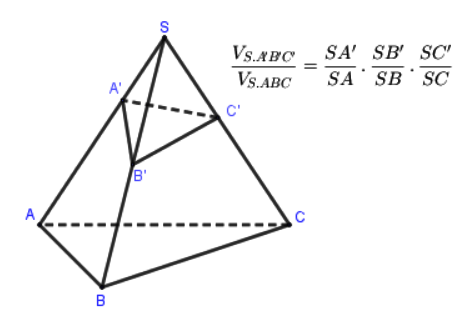
– Tỉ số thể tích hai khối chóp tam giác: Nếu A’, B’, C’ là ba điểm lần lượt nằm trên các cạnh SA, SB, SC của hình chóp tam giác S. ABC. Khi đó:
III. Các dạng toán về hình chóp thường gặp
Phương pháp chung: tính diện tích đáy, các định chiều cao rồi áp dụng công thức
Dạng 1: Tính thể tích khối chóp đều
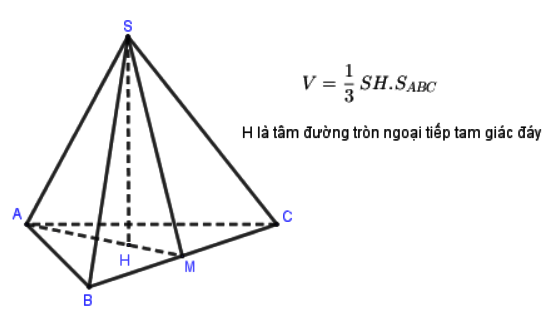
Dạng 2: Tính thể tích khối chóp có mặt bên vuông góc với đáy
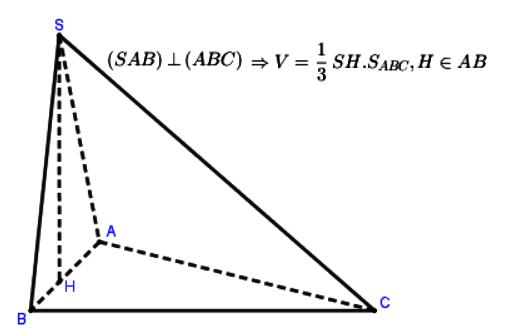
Dạng 3: Tính thể tích hình chóp có cạnh bên vuông góc với đáy
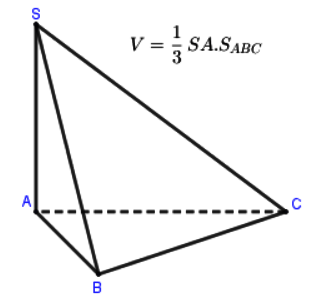
Dạng 4: Tính tỉ số thể tích của khối chóp
– Để tính tỉ số thể tích hai phần của một khối đa diện (H) được phân chia bởi một mặt phẳng (P) ta lựa chọn một trong hai cách:
Cách 1: Ta thực hiện theo các bước:
Bước 1: Dựng thiết diện tạo bởi (P) và (H) chai (H) thành hai hình (H’) và (H’’)
Bước 2: Dùng phương pháp tính thể tích đã biết để tính các thể tích V, V’ của hai hình (H’) và (H’’)
Bước 3: Tính tỉ số V/V’
Cách 2: Sử dụng kết quả:
Trên ba tia không đồng phẳng Sx, Sy, Sz lấy lần lượt các cặp điểm A và A’, B và B’, C và C’ khi đó ta luôn có:
IV. Ví dụ thể tích khối chóp
Bài 1: Cho hình chóp tứ giác đều SABCD có các mặt bên là những tam giác đều, AB=8m, O là trung điểm của AC. Hình chóp SABCD có mấy cạnh? Độ dài SO là bao nhiêu?
Giải:
Hình chóp SABCD là hình chóp tứ giác nên có 8 cạnh.
Hình chóp SABCD đều nên đáy ABCD là hình vuông và tam giác OAB vuông cân tại O.
Áp dụng định lí Py-ta-go vào tam giác vuông OAB có
AB² = OB²+ OB²→ AB² = 2OA²
OA=
Hình chóp có các mặt bên là tam giác đều nên tam giác SAB là tam giác đều. Do đó:
SA = AB = 8m
Ta có SO vuông góc với OA nên tam giác SOA vuông tại O. Áp dụng định lí Py-ta-go ta có:
SB² = OS² + OA²
V. Bài tập thể tích khối chóp
Câu 1: Cho khối chóp S . ABCD có đáy ABCD là hình vuông cạnh a. Biết S A vuông góc với (ABCD) và S A=a sqrt{3}. Thể tích của khối chóp S . ABCD là:
Câu 2: Cho hình chóp tứ giác SABCD có đáy là hình vuông cạnh a, S A vuông góc với mặt phẳng đáy và SA=2 a. Thể tích khối chóp S.ABCD bằng
Câu 3: Cho hình chóp S . ABCD có đáy ABCD là hình chữ nhật A B=a, B C=2 a, cạnh bên S A vuông góc với đáy và
Câu 4: Cho hình chóp S . ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên S A vuông góc với đáy và có độ dài bằng 2 a. Thể tích khối tứ diện S .BCD là:
Câu 5: Cho hình chóp S . ABCD có đáy ABCD là hình vuông tâm O cạnh 2 a. Biết S A vuông góc với mặt phẳng đáy và
Thể tích khối chóp là gì? Công thức tính thể tích khối chóp như thế nào? Mời các bạn hãy cùng Mobitool theo dõi bài viết dưới đây nhé.
Tài liệu Thể tích khối chóp tổng hợp toàn bộ kiến thức như hình chóp là gì, cách tích thể tích hình chóp, các dạng bài tập và ví dụ kèm theo. Thông qua tài liệu này các bạn lớp 12 có thêm nhiều tư liệu tham khảo, trau dồi kiến thức để giải nhanh các bài tập về thể tích khối chóp.
I. Hình chóp là gì?
Hình chóp là hình có mặt đáy là một đa giác và các mặt bên là những tam giác có chung một đỉnh. Đỉnh này được gọi là đỉnh của hình chóp. Đường cao của hình chóp là đường thẳng đi qua đỉnh và vuông góc với mặt phẳng đáy.
Tên gọi của hình chóp dựa vào đa giác đáy: hình chóp tam giác có đáy là tam giác, hình chóp tứ giác có đáy là tứ giác.
II. Công thức thể tích khối chóp

– Công thức thể tích khối chóp
Trong đó: S là diện tích đáy, h là chiều cao khối chóp.
– Một phép vị tự tỉ số k biến khối đa diện có thể tích V thành khối đa diện thể tích V’ thì:
– Tỉ số thể tích hai khối chóp tam giác: Nếu A’, B’, C’ là ba điểm lần lượt nằm trên các cạnh SA, SB, SC của hình chóp tam giác S. ABC. Khi đó:

III. Các dạng toán về hình chóp thường gặp
Phương pháp chung: tính diện tích đáy, các định chiều cao rồi áp dụng công thức
Dạng 1: Tính thể tích khối chóp đều

Dạng 2: Tính thể tích khối chóp có mặt bên vuông góc với đáy

Dạng 3: Tính thể tích hình chóp có cạnh bên vuông góc với đáy

Dạng 4: Tính tỉ số thể tích của khối chóp
– Để tính tỉ số thể tích hai phần của một khối đa diện (H) được phân chia bởi một mặt phẳng (P) ta lựa chọn một trong hai cách:
Cách 1: Ta thực hiện theo các bước:
Bước 1: Dựng thiết diện tạo bởi (P) và (H) chai (H) thành hai hình (H’) và (H’’)
Bước 2: Dùng phương pháp tính thể tích đã biết để tính các thể tích V, V’ của hai hình (H’) và (H’’)
Bước 3: Tính tỉ số V/V’
Cách 2: Sử dụng kết quả:
Trên ba tia không đồng phẳng Sx, Sy, Sz lấy lần lượt các cặp điểm A và A’, B và B’, C và C’ khi đó ta luôn có:
IV. Ví dụ thể tích khối chóp
Bài 1: Cho hình chóp tứ giác đều SABCD có các mặt bên là những tam giác đều, AB=8m, O là trung điểm của AC. Hình chóp SABCD có mấy cạnh? Độ dài SO là bao nhiêu?
Giải:
Hình chóp SABCD là hình chóp tứ giác nên có 8 cạnh.
Hình chóp SABCD đều nên đáy ABCD là hình vuông và tam giác OAB vuông cân tại O.
Áp dụng định lí Py-ta-go vào tam giác vuông OAB có
AB² = OB²+ OB²→ AB² = 2OA²
OA=
Hình chóp có các mặt bên là tam giác đều nên tam giác SAB là tam giác đều. Do đó:
SA = AB = 8m
Ta có SO vuông góc với OA nên tam giác SOA vuông tại O. Áp dụng định lí Py-ta-go ta có:
SB² = OS² + OA²
V. Bài tập thể tích khối chóp
Câu 1: Cho khối chóp S . ABCD có đáy ABCD là hình vuông cạnh a. Biết S A vuông góc với (ABCD) và S A=a sqrt{3}. Thể tích của khối chóp S . ABCD là:
Câu 2: Cho hình chóp tứ giác SABCD có đáy là hình vuông cạnh a, S A vuông góc với mặt phẳng đáy và SA=2 a. Thể tích khối chóp S.ABCD bằng
Câu 3: Cho hình chóp S . ABCD có đáy ABCD là hình chữ nhật A B=a, B C=2 a, cạnh bên S A vuông góc với đáy và
Câu 4: Cho hình chóp S . ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên S A vuông góc với đáy và có độ dài bằng 2 a. Thể tích khối tứ diện S .BCD là:
Câu 5: Cho hình chóp S . ABCD có đáy ABCD là hình vuông tâm O cạnh 2 a. Biết S A vuông góc với mặt phẳng đáy và