You are viewing the article: Lực hướng tâm là gì? Công thức lực hướng tâm và bài tập từ A – Z at Vuidulich.vn
Or you want a quick look: Định nghĩa lực hướng tâm
Trong bài viết dưới đây, điện máy Sharp Việt Nam sẽ chia sẻ lý thuyết lực hướng tâm là gì? Lực hướng tâm xuất hiện khi nào? Công thức lực hướng tâm kèm theo các dạng bài tập có lời giải chi tiết từ A – Z để các bạn cùng tham khảo nhé Vuidulich.vn cũng giúp giải đáp những vấn đề sau đây:
- Ví dụ về lực hướng tâm trong cuộc sống
- Nếu ví dụ về lực hướng tâm
- Chiều của lực hướng tâm
- Bài tập lực hướng tâm
- Thuyết trình bài lực hướng tâm
- Điểm đặt Phương chiều độ lớn của lực hướng tâm
- Khi nào lực hấp dẫn bằng lực hướng tâm
- Hình ảnh lực hướng tâm
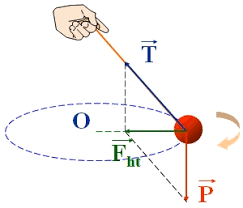
lực hướng tâm
Lực hướng tâm là gì? Công thức tính lực hướng tâm lớp 10
Bài viết hôm nay kienthucviet.vn sẽ chia sẻ công thức lực hướng tâm cùng định nghĩa và một vài ví dụ cho các bạn học sinh tìm hiểu.

 Với:
Với:

Định nghĩa lực hướng tâm
Lực hướng tâm là lực (hay hợp của các lực) tác dụng vào một vật chuyển động tròn đều và gây ra cho vật gia tốc hướng tâm.Công thức lực hướng tâm
 Với:
Với:
- Fht: lực hướng tâm (N)
- aht: gia tốc hướng tâm (m/s2)
- m: khối lượng của vật
- r: bán kính quỹ đạo tròn (m)
- ω: tốc độ góc của chuyển động tròn (rad/s)
- v: tốc độ dài của chuyển động tròn (m/s)
Một vài ví dụ về lực hướng tâm
– Trong hệ qui chiếu gắn với trái đất được coi là đứng yên, lực hấp dẫn giữ cho vệ tinh không bị văng ra khỏi quỹ đạo chuyển động tròn quanh trái đất => lực hấp dẫn đóng vai trò lực hướng tâm. – Một vật được gắn chặt vào đầu một sợi dây sau đó quay nhanh đều sợi dây. Ta thấy vật chuyển động tròn quanh quỹ đạo, nếu buông tay vật sẽ bị văng ra khỏi quỹ đạo tròn => chứng tỏ lực căng của sợi dây đã giữ cho vật chuyển động tròn đều => lực căng đóng vai trò lực hướng tâm. – Đặt một vật lên bàn và bắt đầu quay tròn đều, với vận tốc quay vừa đủ vật vẫn nằm im trên bàn nhờ lực ma sát nghỉ => lực ma sát nghỉ đóng vai trò lực hướng tâm.Vậy ta có kết luận lực hướng tâm là gì?
Lực hướng tâm là tên gọi chung của lực hoặc hợp lực giữ cho vật chuyển động tròn đều quanh quỹ đạo.Chuyển động li tâm
Nếu lực hướng tâm không còn đủ lớn để giữ cho vật chuyển động theo quỹ đạo tròn thì vật sẽ chuyển động li tâm.
Bài tập ứng dụng công thức lực hướng tâm
Bài tập ứng dụng công thức lực hướng tâm Dạng 1: Tính lực hướng tâm Vận dụng các công thức trong chuyển động tròn đều – Công thức chu kì : T = 2π/ω – Công thức tần số: f = 1/T = ω/2π – Công thức tốc độ góc: ω = v/r = 2π/T = f/2π – Lực hướng tâm: Fht = m.aht – Công thức gia tốc hướng tâm: aht = v2/r = r.ω2 – Công thức liên hệ giữa tốc độ dài, tốc độ góc: v = r.ω Ví dụ 1: Xe đạp của 1 vận động viên chuyển động thẳng đều với v = 36 km/h. Biết bán kính của lốp bánh xe đạp là 40 cm. Tính tốc độ góc và gia tốc hướng tâm tại một điểm trên lốp bánh xe. Lời giải Vận tốc xe đạp cũng là tốc độ dài của một điểm trên lốp xe: v = 10 m/s Tốc độ góc là: ω = v/r = 10 : 0,4 = 25 rad/s Gia tốc hướng tâm tại một điểm trên lóp bánh xe là: aht = v2/r = 102/0,4 = 250 m/s2 Ví dụ 2 Vệ tinh A của Việt Nam được phòng lên quỹ đạo ngày 19/4/2008. Sau khi ổn định, vệ tinh chuyển động tròn đều với v = 2.21 km/h ở độ cao 24000km so với mặt đất. Bán kính Trái Đất là 6389 km. Tính tốc độ góc, chu kì, tần số của vệ tinh. Lời giải v = 2,21 km/h = 0,61 m/s r = R + h = 24689 km = 24689.103 m ω = v.r = 15060290 rad/s Chu kì: T = 2π/ω = 2.3,14 : 15060290 = 4.17.10-7s Tần số: f = 1/T = 2398135 vòng/s Ví dụ 3: Một đĩa đồng chất có dạng hình tròn có R = 30 cm đang quay tròn đều quanh trục của nó. Biết thời gian quay hết 1 vòng là 2s. Tính tốc độ dài, tốc độ góc của 2 điểm A, B nằm trên cùng 1 đường kính của đĩa. Biết điểm A nằm trên vành đĩa, điểm B nằm trên trung điểm giữa tâm O của vòng tròn và vành đĩa. Hướng dẫn: RA = 30 cm ⇒ RB = 15 cm Tốc độ góc: ω = 2πT = πrad/s = ωB Ta có: vA = rA.ω = 0.94 m/s; vB = rB.ω = 0.47 m/s Dạng 2: Tính áp lực của vật tại điểm cao nhất của vòng cầu Phương pháp: Bước 1: Xác định véc tơ lực hướng tâm: Vẽ hình, Tìm tất cả các lực tác dụng vào vật chuyển động tròn, Tổng hợp các lực đó theo phương bán kính hướng vào tâm (Tổng hợp véc tơ hay dùng phương pháp chiếu) đó là lực hướng tâm. Bước 2: Viết biểu thức tính độ lớn lực hướng tâm theo m và aht Bước 3: Đồng nhất biểu thức lực và biểu thức độ lớn tìm ẩn số. Cụ thể với bài toán tính áp lực vật tại điểm cao nhất của vòng cầu thì: Cầu vồng lên: N = P – Fht = m.g – m.aht = 0 xe bay khỏi mặt cầu, mặt dốc. Chuyển động của xe đi vào khúc quanh:(mặt đường phải làm nghiêng) lực hướng tâm là hợp lực của phản lực N→ và trọng lực P→ Ví dụ 1: Một xe có khối lượng m = 1 tấn chuyển động qua một chiếc cầu vồng nên với vận tốc v = 10 m/s. Bán kính cong của cầu R = 50 m. Tìm áp lực của xe nên cầu vồng tại : a. Điểm cao nhất cầu. b. Tại nơi bán kính cong hợp với phương thẳng đứng một góc 30°. Lấy g = 10 m/s2 Xe lên cầu với gia tốc a : P→ + N→ = m.aht→ (1) Chiếu (1) nên bán kính ứng với vị trí của xe ta có: Pcosα − N = maht a. Tại điểm cao nhất A của cầu vồng : α = 0 b. Tại vị trí B ứng với α = 30° (hình vẽ) Ví dụ 2: Một ô tô khối lượng 2.5 tấn chuyển động đều qua một đoạn cầu vượt (coi là cung tròn) với vận tốc 54 km/h. Biết bán kính cong của đoạn cầu vượt là 50 m. Lấy g = 9,8 m/s2, bỏ qua ma sát. Hãy xác định áp lực của ô tô lên cầu khi đi qua điểm giữa cầu trong 2 trường hợp: a. Cầu vồng xuống. b. Cầu vồng lên. Lời giải m = 2500 kg v = 54 km/h = 15 m/s g = 9.8 m/s2 R = 50 m a. Khi cầu vồng xuống thì áp lực của ô tô lên cầu là: b. Khi cầu vồng lên thì áp lực của ô tô lên cầu là: Dạng 3: Tính độ biến dạng của lò xo khi vật chuyển động tròn quanh 1 điểm cố định Phương pháp: Lực hướng tâm đóng vai trò là lực đàn hồi Ta áp dụng công thức: Fđh = Fht hoặc Fms = Fht Ví dụ 1: Vật có khối lượng 100g gắn vào đầu lò xo có chiều dài tự nhiên l = 20 cm; k = 20 N/m. Cho hệ lò xo và vật quay đều trên mặt phẳng nằm nghiêng không ma sát v = 60 vòng/phút. Bỏ qua mọi ma sát. Tính độ biến dạng của lò xo. Lời giải Ta có tốc độ góc: ω = 60.( 2π/60) = 2π rad/s Lực đàn hồi đóng vai trò lực hướng tâm: Fđh = Fht Suy ra: kΔl = m.ω2(l + Δl) Vậy Δl = 6.3 .10-3 m Ví dụ 2: Một lò xo có độ cứng k, chiều dài tự nhiên l0 một đầu giữ cố định ở A, đầu kia gắn vào quả cầu khối lượng m có thể trượt không ma sát trên thanh Δ nằm ngang. Thanh Δ quay đều với vận tốc góc w xung quanh trục Δ thẳng đứng. Tính độ dãn của lò xo khi l0 = 20 cm; ω = 20 rad/s; m = 10 g; k = 200 N/m Lời giải Các lực tác dụng vào quả cầu: P→; N→; Fđh→ Trong đó P→ + N→ = 0 nên Fđh→ là lực hướng tâm: k.Δl = m.ω2. (l0 + Δl) ⇒ với k > mω2 Sau khi đọc xong bài viết của chúng tôi các bạn có thể nhớ được công thức lực hướng tâm để áp dụng vào làm bài tập nhé Vuidulich.vn cũng giúp giải đáp những vấn đề sau đây:- Ví dụ về lực hướng tâm trong cuộc sống
- Nếu ví dụ về lực hướng tâm
- Chiều của lực hướng tâm
- Bài tập lực hướng tâm
- Thuyết trình bài lực hướng tâm
- Điểm đặt Phương chiều độ lớn của lực hướng tâm
- Khi nào lực hấp dẫn bằng lực hướng tâm
- Hình ảnh lực hướng tâm
See more articles in the category: Giáo dục