Or you want a quick look: Lý thuyết Bảng lượng giác
Giải bài tập SGK Toán 9 Tập 1 trang 83, 84 để xem gợi ý giải các bài tập của Bài 3: Bảng lượng giác thuộc chương 1 Hình học 9.
Tài liệu được biên soạn với nội dung bám sát chương trình sách giáo khoa Toán lớp 9 tập 1. Qua đó, các em sẽ biết cách giải toàn bộ các bài tập của bài 3 Chương 1 trong sách giáo khoa Toán 9 Tập 1. Chúc các bạn học tốt.
Lý thuyết Bảng lượng giác
1. Cấu tạo của bảng lượng giác
– Bảng sin và côsin (Bảng VIII)
– Bảng tang và côtang (Bảng IX)
– Bảng tang của các góc gần 90° (Bảng X)
Nhận xét:
Khi góc α tăng từ 0° đến 90° (0°<α < 90°) thì sinα và tgα tăng còn cosα và cotgα giảm.
2. Cách dùng bảng, dùng máy tính:
a) Tìm tỉ số lượng giác của một góc nhọn cho trước.
b) Tìm số đo của góc nhọn khi biết một tỷ số lượng giác của góc đó.
Giải bài tập toán 9 trang 83, 84 tập 1
Bài 18 (trang 83 SGK Toán 9 Tập 1)
Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm các tỉ số lượng giác sau (làm tròn đến chữ số thập phân thứ tư):
a) sin 40o12′ ;
b) cos52o54′
c) tg63o36′ ;
d) cotg25o18′
Gợi ý đáp án
a) Dùng bảng lượng giác: sin 40o12′ ≈ 0,6455
– Cách nhấn máy tính:
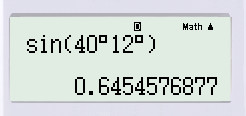
b) cos52o54′ ≈ 0,6032
– Cách nhấn máy tính:
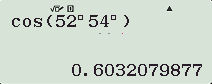
c) tg63o36′ ≈ 2,0145
– Cách nhấn máy tính:
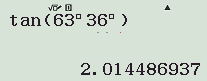
d) cotg25o18′ ≈ 2,1155
– Cách nhấn máy tính:
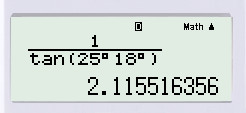
(Lưu ý: Vì trong máy tính không có nút tính cotg nên ta phải tính tg trước rồi nhấn phím nghịch đảo.)
Bài 19 (trang 84 SGK Toán 9 Tập 1)
Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm số đo của góc nhọn x (làm tròn đến phút), biết rằng:
a) sin x = 0,2368 ;
b) cosx = 0,6224
c) tgx = 2,154 ;
d) cotgx = 3,251
Gợi ý đáp án
a) Dùng bảng lượng giác sinx = 0,2368 => x ≈ 13o42′
– Cách nhấn máy tính:
![]()
b) x ≈ 51o31′
– Cách nhấn máy tính:
![]()
c) x ≈ 65o6′
– Cách nhấn máy tính:
![]()
d) x ≈ 17o6′
– Cách nhấn máy tính:
Giải bài tập toán 9 trang 83, 84 tập 1: Luyện tập
Bài 20 (trang 84 SGK Toán 9 Tập 1)
Dùng bảng lượng giác (có sử dụng phần hiệu chỉnh) hoặc máy tính bỏ túi, hãy tìm các tỉ số lượng giác sau (làm tròn đến chữ số thập phân thứ tư) :
Gợi ý đáp án
Cách bấm máy:
![]()
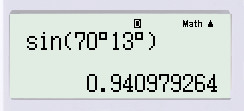
Cách bấm máy:
![]()

Cách bấm máy:
![]()

Cách bấm máy:
![]()
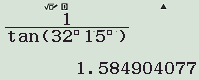
Bài 21 (trang 84 SGK Toán 9 Tập 1)
Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm góc nhọn x (làm tròn kết quả đến độ ), biết rằng:
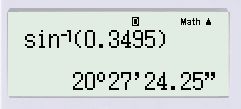
a) sin x = 0,3495;
b) cos x = 0,5427;
c) tg x = 1,5142;
d) cotg x = 3,163
Gợi ý đáp án
Cách bấm máy:
![]()
Cách bấm máy:
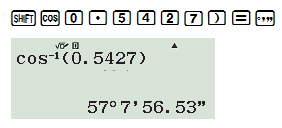
Cách bấm máy:

Cách bấm máy:
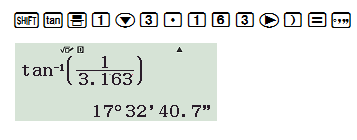
Bài 22 (trang 84 SGK Toán 9 Tập 1)
a) sin 20o và sin 70o ;
b) cos25o và cos63o15′
c) tg 73o20′ và tg 45o ;
d) cotg 2o và cotg 37o40′
Gợi ý đáp án
a) Vì 20o < 70o nên sin 20o < sin70o (góc tăng, sin tăng)
b) Vì 25o < 63o15′ nên cos25o > cos 63o15′ (góc tăng, cos giảm)
c) Vì 73o20′ > 45o nên tg73o20′ > tg45o (góc tăng, tg tăng)
d) Vì 2o < 37o40′ nên cotg 2o > cotg 37o40′ (góc tăng, cotg giảm )
Bài 23 (trang 84 SGK Toán 9 Tập 1)
Tính:
Gợi ý đáp án
a) Ta có:
Do đó
b) Ta có:
Do đó
Nhận xét: Cách giải như trên là dựa vào định lý: nếu hai góc phụ nhau thì sin của góc này bằng côsin của góc kia, tang của góc này bằng côtang của góc kia.
Bài 24 (trang 84 SGK Toán 9 Tập 1)
Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần:
a) sin78o, cos14o, sin 47o, cos87o
b) tg73o, cotg25o, tg62o, cotg38o
Gợi ý đáp án
(Gợi ý: Bài này có 2 cách làm. Cách 1 là sử dụng máy tính. Cách 2 là sử dụng tính chất lượng giác của hai góc phụ nhau để đưa về cùng một tỉ số lượng giác rồi so sánh. Cách 2 nhanh hơn.)
a) Ta có: sin 78o = cos12o; sin 47o = cos 43o
Vì 12o < 14o < 43o < 87o
nên cos 12o > cos 14o > cos 43o > cos 87o
Suy ra: cos 87o < sin47o < cos14o < sin78o
b) Ta có: cotg25o = tg65o; cotg38o = tg52o.
Vậy: cotg38o < tg62o < cotg25o < tg73o
Bài 25 (trang 84 SGK Toán 9 Tập 1)
So sánh:
a) tg25o và sin 25o ;
b) cotg 32o và cos32o
c) tg45o và cos45o ;
d) cotg60o và sin30o
Gợi ý đáp án
a) Ta có
Vì
b) Ta có:
Vì
c) Ta có
Vì
Mà
Vậy
d) Ta có:
Vì
Mà
Do đó
Giải bài tập SGK Toán 9 Tập 1 trang 83, 84 để xem gợi ý giải các bài tập của Bài 3: Bảng lượng giác thuộc chương 1 Hình học 9.
Tài liệu được biên soạn với nội dung bám sát chương trình sách giáo khoa Toán lớp 9 tập 1. Qua đó, các em sẽ biết cách giải toàn bộ các bài tập của bài 3 Chương 1 trong sách giáo khoa Toán 9 Tập 1. Chúc các bạn học tốt.
Lý thuyết Bảng lượng giác
1. Cấu tạo của bảng lượng giác
– Bảng sin và côsin (Bảng VIII)
– Bảng tang và côtang (Bảng IX)
– Bảng tang của các góc gần 90° (Bảng X)
Nhận xét:
Khi góc α tăng từ 0° đến 90° (0°<α < 90°) thì sinα và tgα tăng còn cosα và cotgα giảm.
2. Cách dùng bảng, dùng máy tính:
a) Tìm tỉ số lượng giác của một góc nhọn cho trước.
b) Tìm số đo của góc nhọn khi biết một tỷ số lượng giác của góc đó.
Giải bài tập toán 9 trang 83, 84 tập 1
Bài 18 (trang 83 SGK Toán 9 Tập 1)
Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm các tỉ số lượng giác sau (làm tròn đến chữ số thập phân thứ tư):
a) sin 40o12′ ;
b) cos52o54′
c) tg63o36′ ;
d) cotg25o18′
Gợi ý đáp án
a) Dùng bảng lượng giác: sin 40o12′ ≈ 0,6455
– Cách nhấn máy tính:

b) cos52o54′ ≈ 0,6032
– Cách nhấn máy tính:
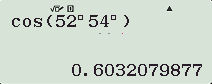
c) tg63o36′ ≈ 2,0145
– Cách nhấn máy tính:
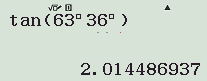
d) cotg25o18′ ≈ 2,1155
– Cách nhấn máy tính:

(Lưu ý: Vì trong máy tính không có nút tính cotg nên ta phải tính tg trước rồi nhấn phím nghịch đảo.)
Bài 19 (trang 84 SGK Toán 9 Tập 1)
Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm số đo của góc nhọn x (làm tròn đến phút), biết rằng:
a) sin x = 0,2368 ;
b) cosx = 0,6224
c) tgx = 2,154 ;
d) cotgx = 3,251
Gợi ý đáp án
a) Dùng bảng lượng giác sinx = 0,2368 => x ≈ 13o42′
– Cách nhấn máy tính:
![]()
b) x ≈ 51o31′
– Cách nhấn máy tính:
![]()
c) x ≈ 65o6′
– Cách nhấn máy tính:
![]()
d) x ≈ 17o6′
– Cách nhấn máy tính:
Giải bài tập toán 9 trang 83, 84 tập 1: Luyện tập
Bài 20 (trang 84 SGK Toán 9 Tập 1)
Dùng bảng lượng giác (có sử dụng phần hiệu chỉnh) hoặc máy tính bỏ túi, hãy tìm các tỉ số lượng giác sau (làm tròn đến chữ số thập phân thứ tư) :
Gợi ý đáp án
Cách bấm máy:
![]()

Cách bấm máy:
![]()

Cách bấm máy:
![]()

Cách bấm máy:
![]()
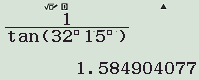
Bài 21 (trang 84 SGK Toán 9 Tập 1)
Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm góc nhọn x (làm tròn kết quả đến độ ), biết rằng:
a) sin x = 0,3495;
b) cos x = 0,5427;
c) tg x = 1,5142;
d) cotg x = 3,163
Gợi ý đáp án
Cách bấm máy:
![]()

Cách bấm máy:

Cách bấm máy:

Cách bấm máy:

Bài 22 (trang 84 SGK Toán 9 Tập 1)
a) sin 20o và sin 70o ;
b) cos25o và cos63o15′
c) tg 73o20′ và tg 45o ;
d) cotg 2o và cotg 37o40′
Gợi ý đáp án
a) Vì 20o < 70o nên sin 20o < sin70o (góc tăng, sin tăng)
b) Vì 25o < 63o15′ nên cos25o > cos 63o15′ (góc tăng, cos giảm)
c) Vì 73o20′ > 45o nên tg73o20′ > tg45o (góc tăng, tg tăng)
d) Vì 2o < 37o40′ nên cotg 2o > cotg 37o40′ (góc tăng, cotg giảm )
Bài 23 (trang 84 SGK Toán 9 Tập 1)
Tính:
Gợi ý đáp án
a) Ta có:
Do đó
b) Ta có:
Do đó
Nhận xét: Cách giải như trên là dựa vào định lý: nếu hai góc phụ nhau thì sin của góc này bằng côsin của góc kia, tang của góc này bằng côtang của góc kia.
Bài 24 (trang 84 SGK Toán 9 Tập 1)
Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần:
a) sin78o, cos14o, sin 47o, cos87o
b) tg73o, cotg25o, tg62o, cotg38o
Gợi ý đáp án
(Gợi ý: Bài này có 2 cách làm. Cách 1 là sử dụng máy tính. Cách 2 là sử dụng tính chất lượng giác của hai góc phụ nhau để đưa về cùng một tỉ số lượng giác rồi so sánh. Cách 2 nhanh hơn.)
a) Ta có: sin 78o = cos12o; sin 47o = cos 43o
Vì 12o < 14o < 43o < 87o
nên cos 12o > cos 14o > cos 43o > cos 87o
Suy ra: cos 87o < sin47o < cos14o < sin78o
b) Ta có: cotg25o = tg65o; cotg38o = tg52o.
Vậy: cotg38o < tg62o < cotg25o < tg73o
Bài 25 (trang 84 SGK Toán 9 Tập 1)
So sánh:
a) tg25o và sin 25o ;
b) cotg 32o và cos32o
c) tg45o và cos45o ;
d) cotg60o và sin30o
Gợi ý đáp án
a) Ta có
Vì
b) Ta có:
Vì
c) Ta có
Vì
Mà
Vậy
d) Ta có:
Vì
Mà
Do đó