Or you want a quick look: Lý thuyết Đường kính và dây của đường tròn
Giải bài tập SGK Toán 9 Tập 1 trang 104 để xem gợi ý giải các bài tập của Bài 2: Đường kính và dây của đường tròn thuộc chương 2 Hình học 9.
Tài liệu được biên soạn với nội dung bám sát chương trình sách giáo khoa Toán lớp 9 tập 1 trang 104. Qua đó, các em sẽ biết cách giải toàn bộ các bài tập của bài Đường kính và dây dẫn của đường tròn Chương 2 trong sách giáo khoa Toán 9 Tập 1. Chúc các bạn học tốt.
Lý thuyết Đường kính và dây của đường tròn
1. So sánh độ dài của đường kính và dây.
Định lý:
Trong các dây của một đường tròn, dây lớn nhất là đường kính.

Xét đường tròn
2. Quan hệ vuông góc giữa đường kính và dây.
Định lý 1:
– Trong một đường tròn, đường kính vuông góc với một dây thì qua trung điểm của dây ấy.
Xét (O,R):
CD là đường kính
AB là dây cung
CD
=> H là trung điểm của AB
Định lý 2: Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
Xét (O,R):
CD là đường kính
AB là dây cung, O
H là trung điểm của AB,
=> CD
Giải bài tập toán 9 trang 104 tập 1
Bài 10 (trang 104 SGK Toán 9 Tập 1)
Cho tam giác ABC, các đường cao BD và CE. Chứng minh rằng:
a) Bốn điểm B, E, D, C cùng thuộc một đường tròn.
b) DE < BC.
Gợi ý đáp án
a) Gọi O là trung điểm của BC
Vì DO là đường trung tuyến của tam giác vuông DBC.
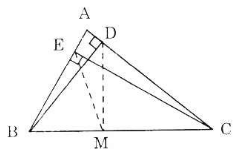
Theo tính chất trung tuyến ứng với cạnh huyền, ta có:
Từ (1) và (2) suy ra OD=OB=OC
Do đó ba điểm B,D, C cùng thuộc đường tròn tâm O bán kính OB.
Lập luận tương tự, tam giác BEC vuông tại E có EO là đường trung tuyến ứng với cạnh huyền BC nên
Suy ra ba điểm B, E, C cùng thuộc đường tròn tâm O bán kính OB.
Do đó 4 điểm B, C, D, E cùng thuộc đường tròn (O) đường kính BC.
b) Xét đường
Ta có DE là một dây cung không đi qua tâm nên ta có BC > DE ( vì trong một đường tròn, dây lớn nhất là đường kính).
Bài 11 (trang 104 SGK Toán 9 Tập 1)
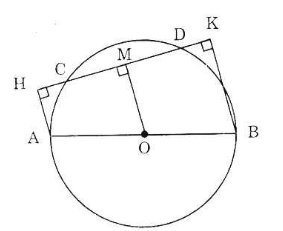
Cho đường tròn (O) đường kính AB, dây CD không cắt đường kính AB, Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ A và B đến CD. Chứng minh rằng CH = DK.
Gợi ý: Kẻ OM vuông góc với CD.
Gợi ý đáp án
Kẻ OM ⊥ CD.
Vì AH // BK (cùng vuông góc HK) nên tứ giác AHKB là hình thang.
Hình thang AHKB có:
AO = OB (bán kính).
OM // AH // BK (cùng vuông góc HK)
=> OM là đường trung bình của hình thang.
=> MH = MK (1)
Vì OM ⊥ CD nên MC = MD (2)
Từ (1) và (2) suy ra CH = DK. (đpcm)
Giải bài tập SGK Toán 9 Tập 1 trang 104 để xem gợi ý giải các bài tập của Bài 2: Đường kính và dây của đường tròn thuộc chương 2 Hình học 9.
Tài liệu được biên soạn với nội dung bám sát chương trình sách giáo khoa Toán lớp 9 tập 1 trang 104. Qua đó, các em sẽ biết cách giải toàn bộ các bài tập của bài Đường kính và dây dẫn của đường tròn Chương 2 trong sách giáo khoa Toán 9 Tập 1. Chúc các bạn học tốt.
Lý thuyết Đường kính và dây của đường tròn
1. So sánh độ dài của đường kính và dây.
Định lý:
Trong các dây của một đường tròn, dây lớn nhất là đường kính.

Xét đường tròn
2. Quan hệ vuông góc giữa đường kính và dây.
Định lý 1:
– Trong một đường tròn, đường kính vuông góc với một dây thì qua trung điểm của dây ấy.
Xét (O,R):
CD là đường kính
AB là dây cung
CD
=> H là trung điểm của AB
Định lý 2: Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
Xét (O,R):
CD là đường kính
AB là dây cung, O
H là trung điểm của AB,
=> CD
Giải bài tập toán 9 trang 104 tập 1
Bài 10 (trang 104 SGK Toán 9 Tập 1)
Cho tam giác ABC, các đường cao BD và CE. Chứng minh rằng:
a) Bốn điểm B, E, D, C cùng thuộc một đường tròn.
b) DE < BC.
Gợi ý đáp án
a) Gọi O là trung điểm của BC
Vì DO là đường trung tuyến của tam giác vuông DBC.

Theo tính chất trung tuyến ứng với cạnh huyền, ta có:
Từ (1) và (2) suy ra OD=OB=OC
Do đó ba điểm B,D, C cùng thuộc đường tròn tâm O bán kính OB.
Lập luận tương tự, tam giác BEC vuông tại E có EO là đường trung tuyến ứng với cạnh huyền BC nên
Suy ra ba điểm B, E, C cùng thuộc đường tròn tâm O bán kính OB.
Do đó 4 điểm B, C, D, E cùng thuộc đường tròn (O) đường kính BC.
b) Xét đường
Ta có DE là một dây cung không đi qua tâm nên ta có BC > DE ( vì trong một đường tròn, dây lớn nhất là đường kính).
Bài 11 (trang 104 SGK Toán 9 Tập 1)
Cho đường tròn (O) đường kính AB, dây CD không cắt đường kính AB, Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ A và B đến CD. Chứng minh rằng CH = DK.
Gợi ý: Kẻ OM vuông góc với CD.
Gợi ý đáp án
Kẻ OM ⊥ CD.
Vì AH // BK (cùng vuông góc HK) nên tứ giác AHKB là hình thang.
Hình thang AHKB có:
AO = OB (bán kính).
OM // AH // BK (cùng vuông góc HK)
=> OM là đường trung bình của hình thang.
=> MH = MK (1)
Vì OM ⊥ CD nên MC = MD (2)
Từ (1) và (2) suy ra CH = DK. (đpcm)
