Or you want a quick look: Giải bài tập toán 8 trang 111, 112 tập 1
Giải bài tập Toán 8 Ôn tập Chương I trang 111, 112 giúp các em học sinh lớp 8 ôn tập, tham khảo gợi ý giải các bài tập trong phần ôn tập chương 1 Hình học 8 tập 1. Từ đó sẽ biết cách giải toàn bộ bài tập ôn tập chương 1.
Giải bài tập toán 8 trang 111, 112 tập 1
Bài 87 (trang 111 SGK Toán 8 Tập 1)
Sơ đồ ở hình 109 biểu thị quan hệ giữa các tập hợp hình thang, hình bình hành, hình chữ nhật, hình thoi, hình vuông. Dựa vào sơ đồ đó, hãy điền vào chỗ trống:
a) Tập hợp các hình chữ nhật là tập hợp con của tập hợp các hình …
b) Tập hợp các hình thoi là tập hợp con của tập hợp các hình …
c) Giao của tập hợp các hình chữ nhật và tập hợp các hình thoi là tập hợp các hình …

Hình 109
Gợi ý đáp án:
a) Tập hợp các hình chữ nhật là tập hợp con của tập hợp các hình bình hành, hình thang.
b) Tập hợp các hình thoi là tập hợp con của tập hợp các hình bình hành, hình thang.
c) Giao của tập hợp các hình chữ nhật và tập hợp các hình thoi là tập hợp các hình vuông.
Bài 88 (trang 111 SGK Toán 8 Tập 1)
Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Các đường chéo AC, BD của tứ giác ABCD có điều kiện gì thì EFGH là:
a) Hình chữ nhật?
b) Hình thoi?
c) Hình vuông?
Gợi ý đáp án:
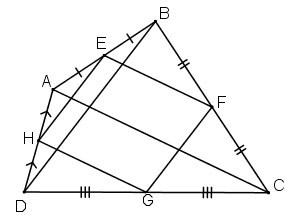
Ta có: EB = EA, FB = FC (gt)
⇒ EF là đường trung bình của ΔABC
⇒ EF // AC và EF =
Ta có: HA = HD, GC = GD
⇒ HG là đường trung bình của ΔADC
⇒ HG // AC và HG =
Do đó EF // HG, EF = HG
⇒ EFGH là hình bình hành.
a) Hình bình hành EFGH là hình chữ nhật ⇔ EH ⊥ EF
⇔ AC ⊥ BD (vì EH // BD, EF// AC)
b) Hình bình hành EFGH là hình thoi
⇔ EF = EH
⇔ AC = BD (Vì EF =
c) EFGH là hình vuông
⇔ EFGH là hình thoi và EFGH là hình chữ nhật
⇔ AC = BD và AC ⊥ DB.
Bài 89 (trang 111 SGK Toán 8 Tập 1)
Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi D là trung điểm của AB, E là điểm dối xứng với M qua D.
a) Chứng minh rằng điểm E đối xứng với điểm M qua AB.
b) Các tứ giác AEMC, AEBM là hình gì? Vì sao?
c) Cho BC = 4cm, tính chu vì tứ giác AEBM.
d) Tam giác vuông ABC có điều kiện gì thì AEBM là hình vuông?
Gợi ý đáp án:
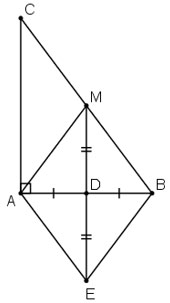
a) Ta có MB = MC, DB = DA
⇒ MD là đường trung bình của ΔABC
⇒ MD // AC
Mà AC ⊥ AB
⇒ MD ⊥ AB.
Mà D là trung điểm ME
⇒ AB là đường trung trực của ME
⇒ E đối xứng với M qua AB.
b) + MD là đường trung bình của ΔABC
⇒ AC = 2MD.
E đối xứng với M qua D
⇒ D là trung điểm EM
⇒ EM = 2.MD
⇒ AC = EM.
Lại có AC // EM
⇒ Tứ giác AEMC là hình bình hành.
+ Tứ giác AEBM là hình bình hành vì có các đường chéo cắt nhau tại trung điểm của mỗi đường.
Hình bình hành AEBM lại có AB ⊥ EM nên là hình thoi.
c) Ta có: BC = 4cm ⇒ BM = 2cm
Chu vi hình thoi AEBM bằng 4.BM = 4.2 = 8cm
d) Hình thoi AEBM là hình vuông ⇔ AB = EM ⇔ AB = AC
Vậy nếu ABC vuông có thêm điều kiện AB = AC (tức tam giác ABC vuông cân tại A) thì AEBM là hình vuông.
Bài 90 (trang 112 SGK Toán 8 Tập 1)
Đố. Tìm trục đối xứng và tâm đối xứng của:
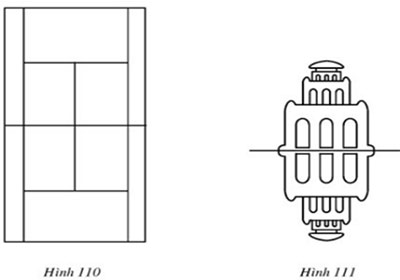
a) Hình 110 (sơ đồ một sân quần vợt)
b) Hình 111 (Tháp Rùa là bóng của nó trên mặt nước)
Gợi ý đáp án:
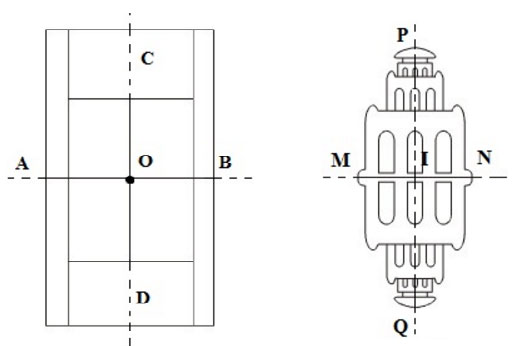
a) Hình 110
– Hai trục đối xứng AB và CD.
– Một tâm đối xứng là O.
b) Hình 111
– Hai trục đối xứng là MN và PQ
– Một tâm đối xứng là I.
Giải bài tập Toán 8 Ôn tập Chương I trang 111, 112 giúp các em học sinh lớp 8 ôn tập, tham khảo gợi ý giải các bài tập trong phần ôn tập chương 1 Hình học 8 tập 1. Từ đó sẽ biết cách giải toàn bộ bài tập ôn tập chương 1.
Giải bài tập toán 8 trang 111, 112 tập 1
Bài 87 (trang 111 SGK Toán 8 Tập 1)
Sơ đồ ở hình 109 biểu thị quan hệ giữa các tập hợp hình thang, hình bình hành, hình chữ nhật, hình thoi, hình vuông. Dựa vào sơ đồ đó, hãy điền vào chỗ trống:
a) Tập hợp các hình chữ nhật là tập hợp con của tập hợp các hình …
b) Tập hợp các hình thoi là tập hợp con của tập hợp các hình …
c) Giao của tập hợp các hình chữ nhật và tập hợp các hình thoi là tập hợp các hình …

Hình 109
Gợi ý đáp án:
a) Tập hợp các hình chữ nhật là tập hợp con của tập hợp các hình bình hành, hình thang.
b) Tập hợp các hình thoi là tập hợp con của tập hợp các hình bình hành, hình thang.
c) Giao của tập hợp các hình chữ nhật và tập hợp các hình thoi là tập hợp các hình vuông.
Bài 88 (trang 111 SGK Toán 8 Tập 1)
Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Các đường chéo AC, BD của tứ giác ABCD có điều kiện gì thì EFGH là:
a) Hình chữ nhật?
b) Hình thoi?
c) Hình vuông?
Gợi ý đáp án:

Ta có: EB = EA, FB = FC (gt)
⇒ EF là đường trung bình của ΔABC
⇒ EF // AC và EF =
Ta có: HA = HD, GC = GD
⇒ HG là đường trung bình của ΔADC
⇒ HG // AC và HG =
Do đó EF // HG, EF = HG
⇒ EFGH là hình bình hành.
a) Hình bình hành EFGH là hình chữ nhật ⇔ EH ⊥ EF
⇔ AC ⊥ BD (vì EH // BD, EF// AC)
b) Hình bình hành EFGH là hình thoi
⇔ EF = EH
⇔ AC = BD (Vì EF =
c) EFGH là hình vuông
⇔ EFGH là hình thoi và EFGH là hình chữ nhật
⇔ AC = BD và AC ⊥ DB.
Bài 89 (trang 111 SGK Toán 8 Tập 1)
Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi D là trung điểm của AB, E là điểm dối xứng với M qua D.
a) Chứng minh rằng điểm E đối xứng với điểm M qua AB.
b) Các tứ giác AEMC, AEBM là hình gì? Vì sao?
c) Cho BC = 4cm, tính chu vì tứ giác AEBM.
d) Tam giác vuông ABC có điều kiện gì thì AEBM là hình vuông?
Gợi ý đáp án:

a) Ta có MB = MC, DB = DA
⇒ MD là đường trung bình của ΔABC
⇒ MD // AC
Mà AC ⊥ AB
⇒ MD ⊥ AB.
Mà D là trung điểm ME
⇒ AB là đường trung trực của ME
⇒ E đối xứng với M qua AB.
b) + MD là đường trung bình của ΔABC
⇒ AC = 2MD.
E đối xứng với M qua D
⇒ D là trung điểm EM
⇒ EM = 2.MD
⇒ AC = EM.
Lại có AC // EM
⇒ Tứ giác AEMC là hình bình hành.
+ Tứ giác AEBM là hình bình hành vì có các đường chéo cắt nhau tại trung điểm của mỗi đường.
Hình bình hành AEBM lại có AB ⊥ EM nên là hình thoi.
c) Ta có: BC = 4cm ⇒ BM = 2cm
Chu vi hình thoi AEBM bằng 4.BM = 4.2 = 8cm
d) Hình thoi AEBM là hình vuông ⇔ AB = EM ⇔ AB = AC
Vậy nếu ABC vuông có thêm điều kiện AB = AC (tức tam giác ABC vuông cân tại A) thì AEBM là hình vuông.
Bài 90 (trang 112 SGK Toán 8 Tập 1)
Đố. Tìm trục đối xứng và tâm đối xứng của:
a) Hình 110 (sơ đồ một sân quần vợt)
b) Hình 111 (Tháp Rùa là bóng của nó trên mặt nước)

Gợi ý đáp án:

a) Hình 110
– Hai trục đối xứng AB và CD.
– Một tâm đối xứng là O.
b) Hình 111
– Hai trục đối xứng là MN và PQ
– Một tâm đối xứng là I.