Or you want a quick look: Lý thuyết bài 1: Tứ giác
Giải bài tập SGK Toán 8 trang 66, 67 giúp các em học sinh lớp 8 xem gợi ý giải các bài tập của Bài 1: Tứ giác Hình học 8 Chương 1. Qua đó các em sẽ nhanh chóng hoàn thiện toàn bộ bài tập của bài 1 Chương I Hình học 8 tập 1.
Lý thuyết bài 1: Tứ giác
Định nghĩa: Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD, DA trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.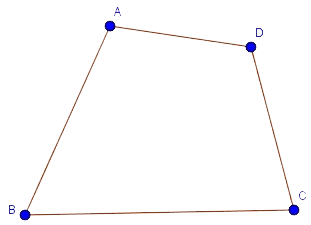
Tứ giác ABCD trên gọi là tứ giác lồi.
Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác.
Giải bài tập toán 8 trang 66, 67 tập 1
Bài 1 (trang 66 SGK Toán 8 Tập 1)
Tìm x ở hình 5, hình 6:
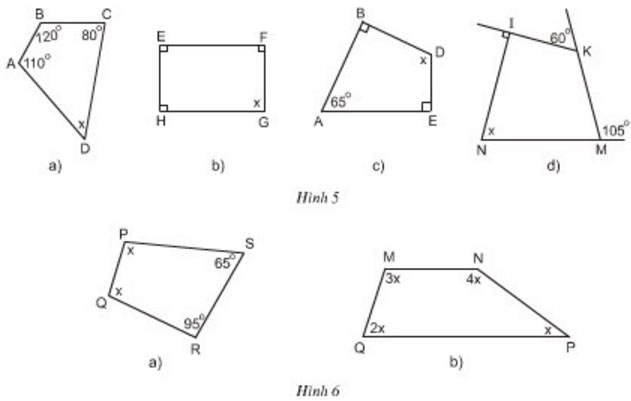
Gợi ý đáp án:
– Hình 5a):
– Hình 5b):
– Hình 5c):
– Hình 5d):
– Hình 6a):
– Hình 6b):
Bài 2 (trang 66 SGK Toán 8 Tập 1)
Góc kề bù của một góc của tứ giác gọi là góc ngoài của tứ giác.
a) Tính góc ngoài của tứ giác ở hình 7a.
b) Tính tổng các góc ngoài của tứ giác ở hình 7b (tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài):
c) Có nhận xét gì về tổng các góc ngoài của tứ giác?
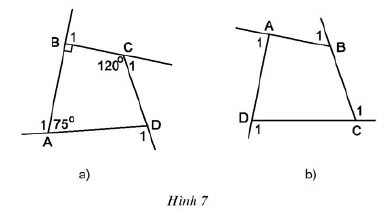
Gợi ý đáp án:
a) Số đo góc còn lại của tứ giác ABCD là:
Góc ngoài của tứ giác tại đỉnh A là:
Góc ngoài của tứ giác tại đỉnh B là:
Góc ngoài của tứ giác tại đỉnh C là:
Góc ngoài của tứ giác tại đỉnh D là:
b) Ta có tổng các góc trong của tứ giác ABCD bằng:
Tổng các góc ngoài của tứ giác ABCD bằng:
c) Như vậy tổng các góc ngoài của tứ giác bằng
Bài 3 (trang 67 SGK Toán 8 Tập 1)
Ta gọi tứ giác ABCD trên hình 8 có AB = AD, CB = CD là hình “cái diều”.
a) Chứng minh rằng AC là đường trung trực của BD
b) Tính
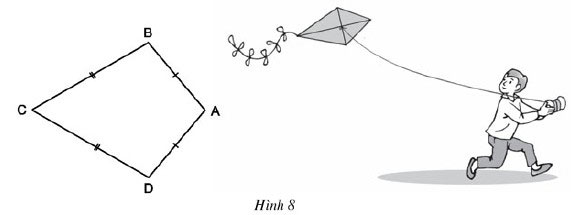
Gợi ý đáp án:
a) Ta có:
AB = AD (gt) ⇒ A thuộc đường trung trực của đoạn thẳng BD
CB = CD (gt) ⇒ C thuộc đường trung trực của đoạn thẳng BD
Nên AC là đường trung trực của đoạn thẳng BD
b)
Suy ra
Ta lại có:
Từ (1) và (2) suy ra
Bài 4 (trang 67 SGK Toán 8 Tập 1)
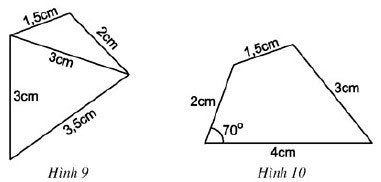
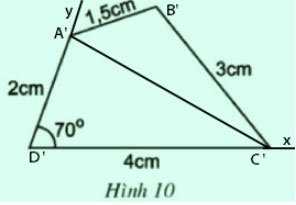
Dựa vào cách vẽ tam giác đã học, hãy vẽ lại các tứ giác ở hình 9, hình 10 vào vở
Gợi ý đáp án:
* Vẽ hình 9:
Trước hết vẽ tam giác ABC:
- Dùng thước đó độ dài vẽ đoạn thẳng AC = 3cm
- Trên cùng một nửa mặt phẳng bờ AC, vẽ cung tròn tâm A bán kính 1,5cm, vẽ cung tròn tâm C bán kính 2cm. Khi đó hai cung tròn cắt nhau tại B
- Nối A với B, C với B ta được tam giác ABC
Tương tự vẽ tam giác ADC:
- Trên cùng một nửa mặt phẳng bờ AC, vẽ cung tròn tâm A bán kính 3cm, vẽ cung tròn tâm C bán kính 3,5cm. Khi đó hai cung tròn cắt nhau tại D
- Nối A với D, C với D ta được tam giác ADC
Tứ giác ABCD là hình cần vẽ.
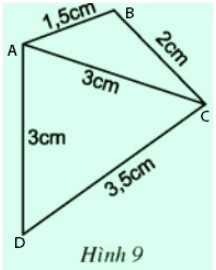
* Vẽ hình 10:
Với hình này ta sẽ vẽ tam giác A’D’C’ trước, bằng cách:
- Dùng thước đo góc vẽ
- Trên tia D’x lấy điểm C’ sao cho D’C’ = 4cm
- Trên tia D’y lấy điểm A’ sao cho D’A’ = 2cm
- Vẽ đoạn thẳng A’C’, ta được tam giác A’D’C’
Vẽ tam giác A’B’C’ giống như cách vẽ tam giác ABC ở hình 9:
- Hai cung tròn tâm A’ bán kính 1,5cm và cung tròn tâm C’ bán kính 3cm cắt nhau tại điểm B’
- Vẽ các đoạn thẳng A’B’, B’C’ ta được tam giác A’B’C’
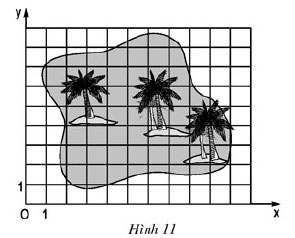
Bài 5 (trang 67 SGK Toán 8 Tập 1)
Đố. Đố em tìm thấy vị trí “kho báu” trên hình 11, biết kho báu nằm tại giao điểm các đường chéo của tứ giác ABCD, trong đó các đỉnh của tứ giác có tọa độ như sau: A(3; 2), B(2; 7), C(6; 8), D(8; 5).
Gợi ý đáp án:
Một bài toán thật thú vị, nào chúng ta cùng đi tìm kho báu thôi:
- Trước hết, với các tọa độ đã cho ta xác định vị trí các điểm A, B, C, D trên hình 11
- Vẽ tứ giác ABCD
- Vẽ hai đường chéo AC, BD. Gọi M là giao điểm của hai đường chéo đó
- Xác định tọa độ điểm M, ta có M(5; 6)
Như vậy kho báu nằm ở tọa độ M(5; 6) trên hình vẽ:
Giải bài tập SGK Toán 8 trang 66, 67 giúp các em học sinh lớp 8 xem gợi ý giải các bài tập của Bài 1: Tứ giác Hình học 8 Chương 1. Qua đó các em sẽ nhanh chóng hoàn thiện toàn bộ bài tập của bài 1 Chương I Hình học 8 tập 1.
Lý thuyết bài 1: Tứ giác
Định nghĩa: Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD, DA trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
Tứ giác ABCD trên gọi là tứ giác lồi.
Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác.
Giải bài tập toán 8 trang 66, 67 tập 1
Bài 1 (trang 66 SGK Toán 8 Tập 1)
Tìm x ở hình 5, hình 6:

Gợi ý đáp án:
– Hình 5a):
– Hình 5b):
– Hình 5c):
– Hình 5d):
– Hình 6a):
– Hình 6b):
Bài 2 (trang 66 SGK Toán 8 Tập 1)
Góc kề bù của một góc của tứ giác gọi là góc ngoài của tứ giác.
a) Tính góc ngoài của tứ giác ở hình 7a.
b) Tính tổng các góc ngoài của tứ giác ở hình 7b (tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài):
c) Có nhận xét gì về tổng các góc ngoài của tứ giác?

Gợi ý đáp án:
a) Số đo góc còn lại của tứ giác ABCD là:
Góc ngoài của tứ giác tại đỉnh A là:
Góc ngoài của tứ giác tại đỉnh B là:
Góc ngoài của tứ giác tại đỉnh C là:
Góc ngoài của tứ giác tại đỉnh D là:
b) Ta có tổng các góc trong của tứ giác ABCD bằng:
Tổng các góc ngoài của tứ giác ABCD bằng:
c) Như vậy tổng các góc ngoài của tứ giác bằng
Bài 3 (trang 67 SGK Toán 8 Tập 1)
Ta gọi tứ giác ABCD trên hình 8 có AB = AD, CB = CD là hình “cái diều”.
a) Chứng minh rằng AC là đường trung trực của BD
b) Tính

Gợi ý đáp án:
a) Ta có:
AB = AD (gt) ⇒ A thuộc đường trung trực của đoạn thẳng BD
CB = CD (gt) ⇒ C thuộc đường trung trực của đoạn thẳng BD
Nên AC là đường trung trực của đoạn thẳng BD
b)
Suy ra
Ta lại có:
Từ (1) và (2) suy ra
Bài 4 (trang 67 SGK Toán 8 Tập 1)
Dựa vào cách vẽ tam giác đã học, hãy vẽ lại các tứ giác ở hình 9, hình 10 vào vở

Gợi ý đáp án:
* Vẽ hình 9:
Trước hết vẽ tam giác ABC:
- Dùng thước đó độ dài vẽ đoạn thẳng AC = 3cm
- Trên cùng một nửa mặt phẳng bờ AC, vẽ cung tròn tâm A bán kính 1,5cm, vẽ cung tròn tâm C bán kính 2cm. Khi đó hai cung tròn cắt nhau tại B
- Nối A với B, C với B ta được tam giác ABC
Tương tự vẽ tam giác ADC:
- Trên cùng một nửa mặt phẳng bờ AC, vẽ cung tròn tâm A bán kính 3cm, vẽ cung tròn tâm C bán kính 3,5cm. Khi đó hai cung tròn cắt nhau tại D
- Nối A với D, C với D ta được tam giác ADC
Tứ giác ABCD là hình cần vẽ.

* Vẽ hình 10:
Với hình này ta sẽ vẽ tam giác A’D’C’ trước, bằng cách:
- Dùng thước đo góc vẽ
- Trên tia D’x lấy điểm C’ sao cho D’C’ = 4cm
- Trên tia D’y lấy điểm A’ sao cho D’A’ = 2cm
- Vẽ đoạn thẳng A’C’, ta được tam giác A’D’C’
Vẽ tam giác A’B’C’ giống như cách vẽ tam giác ABC ở hình 9:
- Hai cung tròn tâm A’ bán kính 1,5cm và cung tròn tâm C’ bán kính 3cm cắt nhau tại điểm B’
- Vẽ các đoạn thẳng A’B’, B’C’ ta được tam giác A’B’C’

Bài 5 (trang 67 SGK Toán 8 Tập 1)
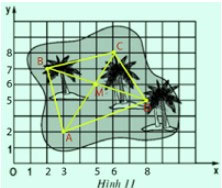
Đố. Đố em tìm thấy vị trí “kho báu” trên hình 11, biết kho báu nằm tại giao điểm các đường chéo của tứ giác ABCD, trong đó các đỉnh của tứ giác có tọa độ như sau: A(3; 2), B(2; 7), C(6; 8), D(8; 5).

Gợi ý đáp án:
Một bài toán thật thú vị, nào chúng ta cùng đi tìm kho báu thôi:
- Trước hết, với các tọa độ đã cho ta xác định vị trí các điểm A, B, C, D trên hình 11
- Vẽ tứ giác ABCD
- Vẽ hai đường chéo AC, BD. Gọi M là giao điểm của hai đường chéo đó
- Xác định tọa độ điểm M, ta có M(5; 6)
Như vậy kho báu nằm ở tọa độ M(5; 6) trên hình vẽ:
