Công thức tính diện xung quanh, diện tích toàn phần và thể tích hình nón là những công thức cơ bản nhất của toán học, góp phần quan trọng vào việc thiết kế cũng như ngành kĩ thuật. Sau đây chúng ta sẽ tìm hiểu cách tính các diện tích, thể tích hình nón và các ví dụ liên quan nhé!
1. Hình nón là gì?
Hình nón là hình hình học không gian 3 chiều đặc biệt có bề mặt phẳng và bề mặt cong hướng về phía trên. Đầu nhọn của hình nón được gọi là đỉnh, bề mặt phẳng được gọi là đáy. Trong thực tế, những vật dụng có dạng hình nón như là chiếc nón lá, cây kem, chiếc mũ sinh nhật.

Hình nón có 3 thuộc tính chính gồm:
+ Có một đỉnh hình tam giác.
+ Một mặt tròn gọi là đáy hình nón.
+ Đặc biệt nó không có bất kỳ cạnh nào.
+ Chiều cao (h) – Chiều cao là khoảng cách từ tâm của vòng tròn đến đỉnh của hình nón. Hình tạo bởi đường cao và bán kính trong hình nón là một tam giác vuông.
2. Công thức tính diện tích hình nón
– Công thức tính diện tích xung quanh hình nón
Diện tích xung quanh hình nón chỉ bao gồm diện tích mặt xung quanh, bao quanh hình nón, không gồm diện tích đáy.
+ Công thức
Diện tích xung quanh của hình nón tròn xoay bằng một nửa tích độ dài đường tròn đáy và độ dài đường sinh.
Sxq = π.r.l
Trong đó:
Sxq : Kí hiệu diện tích xung quanh hình nón.
r: Bán kính mặt đáy của hình nón.
π: Hằng số (π ≈ 3,14).
l: Độ dài đường sinh.
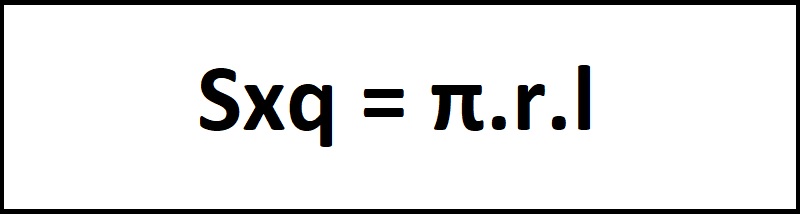
+ Ví dụ
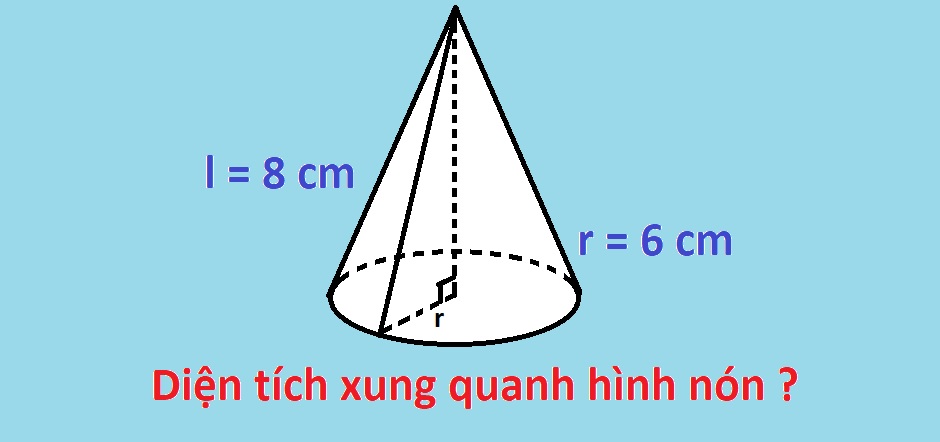
Cho một hình nón bất kỳ có đáy là tâm O và đỉnh A. Bán kính r nối từ tâm đáy hình nón tới một cạnh đáy bất kỳ của hình nón dài 6 cm, chiều dài đường sinh nối từ đỉnh A xuống một điểm bất kỳ trên đáy dài 8 cm. Hỏi diện tích xung quanh hình nón bằng bao nhiêu?
Áp dụng công thức : Sxq = π.r.l = π x 8 x 6 = 48π (cm)².
– Công thức tính diện tích toàn phần hình nón
Diện tích toàn phần được tính là độ lớn của toàn bộ không gian hình chiếm giữ, bao gồm cả diện tích xung quanh và diện tích đáy tròn.
+ Công thức
Diện tích toàn phần hình nón bằng diện tích xung quang hình nón công với diện tích mặt đáy hình nón.
Stp = Sxq + Sđáy
Stp = π.r.l + π.r2
Trong đó:
Stp: Diện tích toàn phần hình nón.
Sxq: Diện tích xung quanh hình nón.
Sđáy: Diện tích đáy của hình nón.
π: Hằng số Pi (π ≈ 3,14).
r: Bán kính đáy hình nón.
l: Độ dài đường sinh hình nón.
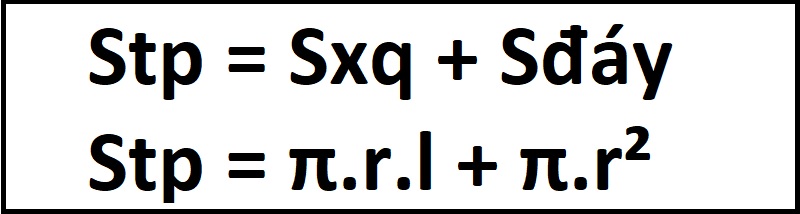
+ Ví dụ
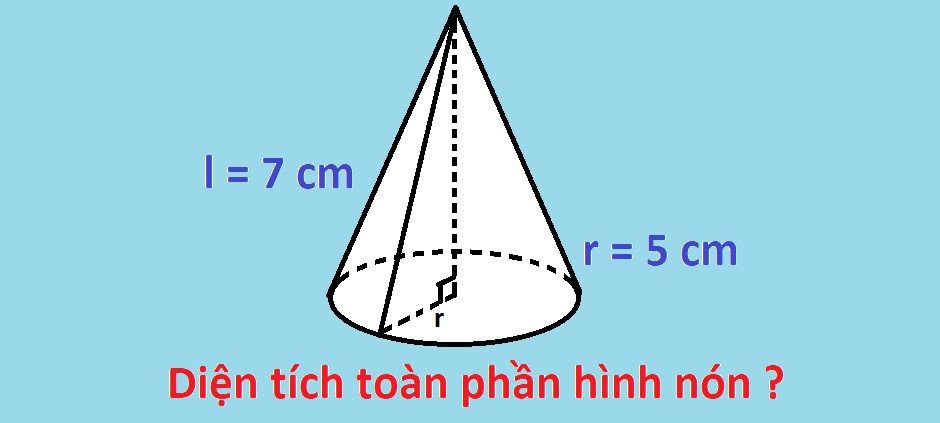
Cho một hình nón bất kỳ có đáy là tâm O và đỉnh A. Bán kính r nối từ tâm đáy hình nón tới một cạnh đáy bất kỳ của hình nón dài 5cm. Hỏi diện tích toàn phần của hình nón bằng bao nhiêu, biết chiều dài đường sinh nối từ đỉnh A xuống một điểm bất kỳ trên đáy dài 7cm.
Hướng dẫn giải:
Áp dụng công thức: Stp = π.r.l + π.r² = π x 5 x 7 + π x 5² = 60π (cm)².
3. Công thức tính thể tích hình nón
Thể tích hình nón là lượng không gian mà hình nón chiếm.
– Công thức
Thể tích hình nón bằng 1/3 diện tích của mặt đáy nhân với chiều cao.
V = 1/3.π.r2 .h
Trong đó:
V:Thể tích hình nón.
r:Bán kính đáy ủa hình nón.
h:Chiều cao, khoảng cách giữa đỉnh và đáy của hình nón.
Đơn vị đo: m3 (mét khối)

– Ví dụ
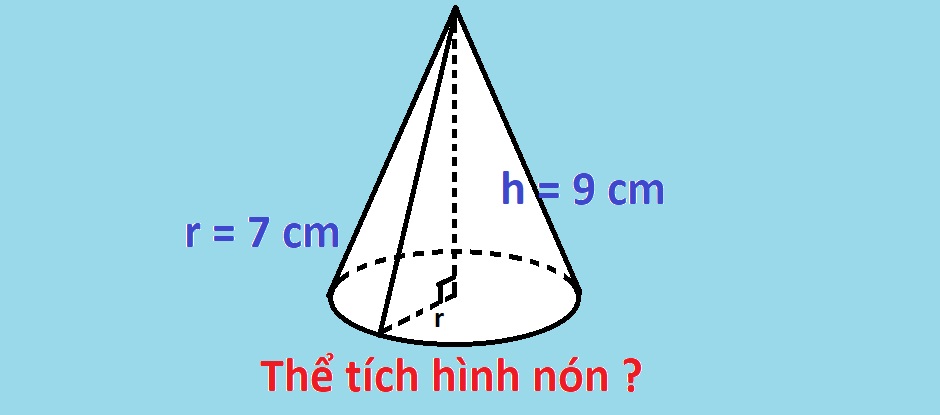
Cho một hình nón bất kỳ có đáy là tâm O và đỉnh A. Bán kính r nối từ tâm đáy hình nón tới một cạnh đáy bất kỳ của hình nón dài 7cm, chiều cao nối từ tâm đáy tới đỉnh của hình nón dài 9cm. Hỏi thể tích hình nón này bằng bao nhiêu?
Hướng dẫn giải:
Sử dụng công thức tính thể tích hình nón trên, ta có thể tích hình nón trên:
V = 1/3 x π x r2 x h = 1/3 x π x (7×7) x 9 = 149π (m3).
Một số sản phẩm máy tính cầm tay giúp bạn tính toán dễ dàng hơn:
Hy vọng qua bài viết này các bạn sẽ nhớ công thức diện tích xung quanh, toàn phần và thể tích hình nón.