Or you want a quick look: I. CẤP SỐ CỘNG VÀ CẤP SỐ NHÂN LÀ GÌ
Có những công thức cấp số cộng và cấp số nhân nào? Bài viết dưới đây tôi sẽ hướng dẫn các bạn các công thức liên quan đến 2 dãy số này. Đồng thời cũng lưu ý cho các bạn công thức nào cần nhớ và được sử dụng nhiều hơn. Bên cạnh đó sẽ có các ví dụ minh họa rõ ràng.
I. CẤP SỐ CỘNG VÀ CẤP SỐ NHÂN LÀ GÌ
- Cấp số cộng là 1 dãy số (hữu hạn hoặc vô hạn) thỏa mãn điều kiện: Kể từ số hạng thứ 2 trở đi đều bằng số hạng đứng trước nó cộng với 1 số không đổi. Số không đổi đó gọi là công sai.
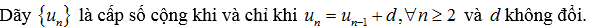
Ví dụ:
Dãy số 1; 3; 5; 7 là một cấp số cộng.
Vì 3=1+2; 5=3+2; 7=5+2 nên đây là cấp số cộng với công sai d=2.
- Trường hợp đặc biệt của cấp số cộng:
Nếu công sai bằng 0 thì cấp số cộng là 1 dãy hằng.
Chẳng hạn 1; 1; 1; … là cấp số cộng với công sai bằng 0.
- Cấp số nhân là 1 dãy số (hữu hạn hoặc vô hạn) thỏa mãn điều kiện: Kể từ số hạng thứ 2 trở đi đều bằng số hạng đứng trước nó nhân với 1 số không đổi. Số không đổi đó gọi là công bội.
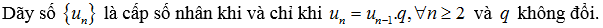
Ví dụ:
Dãy số 2; 4; 8;16 là một cấp số nhân.
Vì 4=2.2; 8=4.2; 16=8.2 nên đây là cấp số nhân với công bội q=2.
- Một số trường hợp đặc biệt của cấp số nhân:
Nếu công bội bằng 0 thì từ số hạng thứ 2 trở đi của cấp số nhân đều bằng 0.
Nếu công bội bằng 1 thì cấp số nhân là dãy hằng. Khi đó cấp số nhân đồng thời là cấp số cộng với công sai bằng 0.
Nếu cấp số nhân có số hạng đầu bằng 0 thì cấp số nhân là dãy hằng 0.
Nếu cấp số nhân vô hạn số hạng có công bội q thỏa mãn -1<q<1 thì cấp số nhân đó được gọi là cấp số nhân lùi vô hạn.
II. CÔNG THỨC CẤP SỐ CỘNG VÀ CẤP SỐ NHÂN
Các công thức cấp số cộng cấp số nhân là các công thức liên quan tới các giá trị đặc trưng của 2 loại dãy số đó.
Các giá trị đặc trưng bao gồm: Số hạng đầu; Số hạng thứ n; Công bội của cấp số nhân; Công sai của cấp số cộng; Tổng của n số dạng đầu; Số hạng đứng giữa hai số hạng khác. Sau đây chúng ta cùng tìm hiểu chi tiết từng công thức nhé.
1. CÔNG THỨC CẤP SỐ CỘNG
Công thức 1: Trước tiên chúng ta nên nhớ công thức tổng quát này:
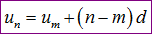
Công thức này tổng quát cho công thức
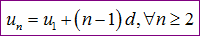
đã có trong sách giáo khoa.
Cũng từ đó ta suy ra được công thức: Từ số hạng thứ 2 trở đi của cấp số cộng đều bằng trung bình cộng của 2 số hạng liền kề với nó.
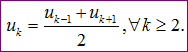
Ví dụ:
Tìm số hạng thứ 2 của cấp số cộng biết số hạng thứ 7 là 100 và công sai là 2.
Lời giải:
Áp dụng công thức trên ta có số hạng thứ 2 của cấp số cộng là:
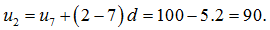
Công thức 2: Với cấp số cộng thì chúng ta có tới 2 công thức để tính tổng của n số hạng đầu. Nhưng ta chỉ nên nhớ công thức:
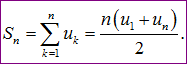
Sau đó thay công thức 1 vào ta sẽ có công thức:
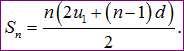
Ví dụ:
Cho cấp số cộng có số hạng đầu bằng 3 và công sai bằng 2. Tính tổng 20 số hạng đầu của cấp số cộng.
Lời giải:
Áp dụng công thức ta có:
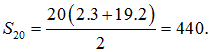
2. CÔNG THỨC CẤP SỐ NHÂN
Các cấp số nhân đặc biệt có công bội bằng 1 thì đồng thời cũng là cấp số cộng. Vì vậy với các dãy số này ta dùng công thức của cấp số cộng nhé.Còn với cấp số nhân có công bội bằng 0 thì các số hạng là: u(1);0 ;0 … Nói chung không có “cóc khô” gì để mà bàn thêm :)).
Vì vậy ở đây chúng ta xét các cấp số nhân mà công bội và số hạng đầu khác 0. Điều đó cũng có nghĩa tất cả các số hạng của cấp số nhân khác 0.
Công thức 1:
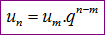
Ví dụ:
Tính số hạng thứ 5 của cấp số nhân biết số hạng thứ 8 của cấp số nhân bằng 32 và công bội bằng 2.
Lời giải:
Áp dụng công thức ta có:
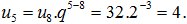
Từ công thức trên ta dễ dàng suy ra được các công thức:
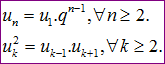
Công thức 2:
Tổng của n số hạng đầu của cấp số nhân được tính theo công thức:
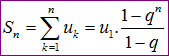
Ví dụ:
Cho cấp số nhân có số hạng đầu bằng 2. Tính tổng 11 số hạng đầu của cấp số nhân.
Lời giải:
Áp dụng công thức ta có:
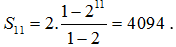
Trên đây, tôi đã giới thiệu đến các bạn công thức cấp số cộng, công thức cấp số nhân(các công thức đóng khung màu tím) cùng 1 số ví dụ đơn giản . Hãy luyện tập để thành thạo nhé. Chúc các bạn học giỏi và thành công!
Xem thêm:
Cấp số cộng, công sai là gì? Lý thuyết và công thức tính cấp số cộng
Cấp số nhân, công bội là gì? Lý thuyết và công thức tính cấp số nhân