Bài viết này chúng ta cùng ôn lại công thức tính khoảng cách giữa 2 điểm, từ điểm tới đường thẳng, qua đó vận dụng giải một số bài tập minh họa để các em hiểu rõ cách vận dụng công thức tính này.
I. Công thức tính khoảng cách giữa 2 điểm
– Cho điểm A(xA; yA) và điểm B(xB; yB), khoảng cách giữa hai điểm này là:
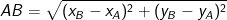
II. Công thức tính khoảng cách từ điểm tới đường thẳng
– Cho đường thẳng Δ: Ax + By + C = 0 và điểm M0(x0; y0). Khi đó khoảng cách từ điểm M0 đến đường thẳng Δ là:
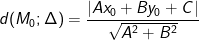
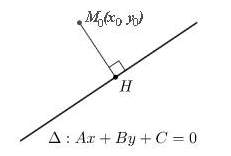
– Khoảng cách từ điểm M0 đến đường thẳng Δ là độ dài của đoạn thẳng M0H (trong đó H là hình chiếu vuông góc của M0 lên Δ).> Lưu ý: Trong trường hợp đường thẳng Δ chưa viết dưới dạng tổng quát thì đầu tiên ta cần đưa đường thẳng Δ về dạng tổng quát.
III. Tính khoảng cách giữa 2 điểm, từ điểm tới đường thẳng qua bài tập minh họa
* Ví dụ 1: Trong mặt phẳng Oxy cho điểm A(1;2) và điểm B(-3;4). Tính độ dài đoạn thẳng AB.
* Lời giải:
– Độ dài đoạn thẳng AB là khoảng cách giữa 2 điểm A,B ta có:
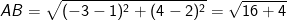
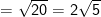
* Ví dụ 2: Tính khoảng cách từ điểm M(2;-1) đến đường thẳng (Δ): 3x + 4y + 7 = 0.
* Lời giải:
– Khoảng cách từ điểm M đến đường thẳng (Δ) là:
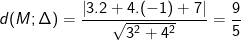
* Ví dụ 3: Tính khoảng cách từ điểm A(0;1) đến đường thẳng (Δ): 4x + 3y = 6
* Lời giải:
– Đường thẳng (Δ): 4x + 3y = 6 ⇔ 4x + 3y – 6 = 0
– Khoảng cách từ điểm A đến (Δ) là:
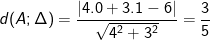
* Ví dụ 4: Tính khoảng cách từ điểm M(1;1) đến đường thẳng (Δ) có phương trình tham số: x = 3 + 3t và y = 2 + t.
* Lời giải:
– Ta cần đưa phương trình đường thẳng (Δ) về dạng tổng quát.
– Ta có: (Δ) đi qua điểm A(3;2) và có VTCP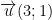 
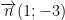
⇒ VTPT 
⇒ Phương trình (Δ): 1.(x – 3) – 3(y – 2) = 0 ⇔ x – 3y + 3 = 0
⇒ Khoảng cách từ điểm M(1;1) đến (Δ) là:
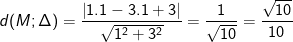
* Ví dụ 5: Đường tròn (C) có tâm là gốc tọa độ O(0; 0) và tiếp xúc với đường thẳng (Δ): 4x – 3y + 25 = 0. Bán kính R của đường tròn (C) bằng:
* Lời giải:
– Do đường thẳng (Δ) tiếp xúc với đường tròn (C) nên khoảng cách từ tâm đường tròn đến đường thẳng (Δ) chính là bán kính R của đường tròn.
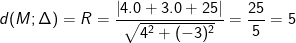
* Ví dụ 6: Khoảng cách từ giao điểm của hai đường thẳng (d1): x – 3y + 4 = 0 và(d2): 2x + 3y – 1 = 0 đến đường thẳng ∆: 3x + y + 16 = 0 bằng:
* Lời giải:
– Trước hết ta cần tìm giao điểm của (d1) và (d2); từ đó tính khoảng cách từ giao điểm này tới (∆).
– Giả sử giao điểm của (d1) và (d2) là A thì tọa độ của A là nghiệm của hệ phương trình:
x – 3y + 4 = 0 và 2x + 3y – 1 = 0
Giải hệ được x = -1 và y = 1 ⇒ A(-1;1)
– Khoảng cách từ điểm A(-1;1) đến đường thẳng ∆: 3x + y + 16 = 0 là:
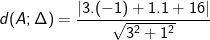
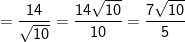
* Ví dụ 7: Trong mặt phẳng hệ tọa độ Oxy, cho tam giác ABC có A(1;1); B(0;3) và C(4;0).
a) Tính chiều dài đường cao AH (H thuộc BC).
b) Tính diện tích tam giác ABC
* Lời giải:
a) Tính chiều dài đường cao AH
– Chiều dài đường cao AH chính là khoảng cách từ A tới đường thẳng BC. Vì vậy ta cần viết phương trình dường thẳng BC từ đó tính khoảng cách từ A tới BC.
– PT đường thẳng BC: Đi qua B(0;3) và có CTCP BC(xC – xB; yC – yB) = (4;-3) nên VTPT là n(3;4).
⇒ PTĐT (BC) là: 3(x – 0) + 4( y – 3) = 0 ⇔ 3x + 4y – 12 = 0
⇒ chiều cao của tam giác kẻ từ đỉnh A chính là khoảng cách từ điểm A đến đường thẳng BC:
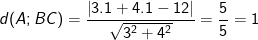
b) Tính diện tích tam giác ABC.
– Ta có: SΔABC = (1/2).AH.BC
– Có độ dài BC là:
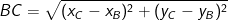
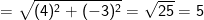
– Mà AH = d(A;BC) = 1 (theo câu a)
⇒ SΔABC = (1/2)mobitool.net = (1/2).1.5 = 5/2 =2,5.
