Giải Toán 9 Bài 2: Hàm số bậc nhất

You are viewing the article: Giải Toán 9 Bài 2: Hàm số bậc nhất at Vuidulich.vn

Or you want a quick look: Lý thuyết Hàm số bậc nhất

Giải bài tập SGK Toán 9 Tập 1 trang 48 để xem gợi ý giải các bài tập của Bài 2: Hàm số bậc nhất thuộc chương 2 Đại số 9.

Tài liệu được biên soạn với nội dung bám sát chương trình sách giáo khoa Toán lớp 9 tập 1 trang 48. Qua đó, các em sẽ biết cách giải toàn bộ các bài tập của bài 2 Chương 2 trong sách giáo khoa Toán 9 Tập 1. Chúc các bạn học tốt.

Lý thuyết Hàm số bậc nhất

1. Định nghĩa

– Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b trong đó a, b là các số thực cho trước và a ≠ 0

– Đặc biệt, khi b = 0 thì hàm số bậc nhất trở thành hàm số y = ax, biểu thị tương quan tỉ lệ thuận giữa y và x

2. Tính chất

a) Hàm số bậc nhất y = ax + b xác định với mọi giá trị x ∈ R

b) Trên tập hợp số thực R, hàm số y = ax + b đồng biến khi a > 0 và nghịch biến khi a < 0

Hàm số y = f(x) gọi là đồng biến trong khoảng nào đó nếu với mọi x₁ và x₂ trong khoảng đó sao cho x₁ < x₂ thì f(x₁ ) < f(x₂ )

Hàm số y = f(x) gọi là nghịch biến trong khoảng nào đó nếu với mọi x₁ và x₂ trong khoảng đó sao cho x₁ < x₂ thì f(x₁ ) > f(x₂ )

3. Nhận xét về đồ thị hàm số y = ax + b (a ≠ 0)

a) Đồ thị hàm số y = ax (a ≠ 0) là một đường thẳng đi qua gốc tọa độ mà ta gọi là đường thẳng y = ax. Đường thẳng y = ax nằm ở góc phần tư thứ I và thứ III khi a > 0; nằm ở góc phần tư thứ II và thứ IV khi a < 0

b) Đồ thị của hàm số y = ax + b là một đường thẳng cắt trục tung tại điểm có tung độ bằng b và song song với đường thẳng y = ax nếu b ≠ 0; trùng với đường thẳng y = ax nếu b = 0.

Đồ thị của hàm số bậc nhất y = ax + b (a ≠ 0) còn gọi là đường thẳng y = ax + b; b được gọi là tung độ gốc của đường thẳng.

Giải bài tập toán 9 trang 48 tập 1

Bài 8 (trang 48 SGK Toán 9 Tập 1)

Trong các hàm số sau, hàm số nào là hàm số bậc nhất? Hãy xác định các các hệ số a, b của chúng và xét xem hàm số bậc nhất này đồng biến hay nghịch biến?

READ Tiếng Anh 6 Unit 1: Writing

a) y = 1 – 5x ;

b) y = -0,5x

c) y = √2(x – 1) + √3 ;

d) y = 2×2 + 3

Gợi ý đáp án

a) y = 1 – 5x là hàm số bậc nhất có a = -5, b = 1, nghịch biến vì a = -5 < 0

b) y = -0,5x là hàm số bậc nhất có a = -0,5, b = 0, nghịch biến vì a = -0,5 < 0

c) y = √2(x – 1) + √3 = √2 x + √3 – √2 là hàm số bậc nhất có a = √2, b = √3 – √2, đồng biến vì a = √2 > 0

d) y = 2×2 + 3 không phải là hàm số bậc nhất (vì số mũ của x là 2)

Bài 9 (trang 48 SGK Toán 9 Tập 1)

Cho hàm số bậc nhất y = (m – 2)x + 3. Tìm các giá trị của m để hàm số:

a) Đồng biến

b) Nghịch biến

Gợi ý đáp án

Hàm số y = ax + b đồng biến khi a > 0 và nghịch biến khi a < 0.)

a) y = (m – 2)x + 3 đồng biến khi m – 2 > 0 ⇔ m > 2

Vậy với m > 2 thì hàm số đồng biến.

b) y = (m – 2)x + 3 nghịch biến khi m – 2 < 0 ⇔ m < 2

Vậy với m < 2 thì hàm số nghịch biến.

Bài 10 (trang 48 SGK Toán 9 Tập 1)

Một hình chữ nhật có các kích thước là 20cm và 30cm. Người ta bớt mỗi kích thước của nó đi x (cm) được hình chữ nhật mới có chu vi là y (cm). Hãy lập công thức tính y theo x.

Gợi ý đáp án

Theo bài ra ta vẽ hình sau:

– Gọi hình chữ nhật ban đầu ABCD có kích thước AB = 30cm; BC = 20cm.

– Sau khi bớt các kích thước của hình chữ nhật đi x (cm), ta có hình chữ nhật mới là A’B’C’D’ có:

A’B’ = 30 – x

B’C’ = 20 – x

Gọi y là chu vi của hình chữ nhật A’B’C’D’, ta có:

y = 2[(30 – x) + (20 – x)]

=> y = 2(50 – 2x)

=> y = -4x + 100 (cm)

Giải bài tập toán 9 trang 48 tập 1: Luyện tập

Bài 11 (trang 48 SGK Toán 9 Tập 1)

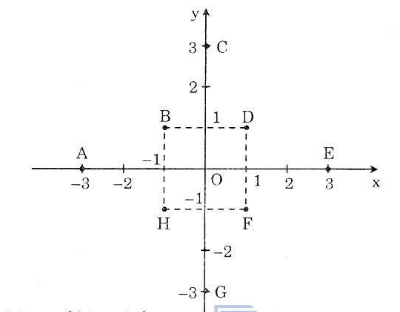
Hãy biểu diễn các điểm sau trên mặt phẳng tọa độ: A(-3; 0), B(-1; 1), C(0; 3), D(1; 1), E(3; 0), F(1; -1), G(0; 3), H(-1; -1).

Gợi ý đáp án

Biểu diễn các điểm trên mặt phẳng tọa độ: A(-3; 0), B(-1; 1), C(0; 3), D(1; 1), E(3; 0), F(1; -1), G(0; 3), H(-1; -1). như hình vẽ sau:

Bài 12 (trang 48 SGK Toán 9 Tập 1)

Cho hai hàm số bậc nhất y = ax + 3. Tìm hệ số a, biết rằng khi x = 1 thì y = 2,5.

Gợi ý đáp án

Thay x = 1, y = 2,5 vào y = ax + 3 ta được:

2,5 = a.1 + 3

=> a = 2,5 – 3 = -0,5

Vậy a = -0,5

Bài 13 (trang 48 SGK Toán 9 Tập 1)

Với những giá trị nào của m thì mỗi hàm số sau là hàm số bậc nhất ?

$a) y=sqrt{5 - m}(x - 1);$

$b) y = dfrac{m + 1}{m - 1}x +3,5$

Gợi ý đáp án

a) Ta có $y=sqrt{5 - m}(x - 1) Leftrightarrow y=sqrt{5 - m}.x - sqrt{5 - m}$

Hệ số là $a=sqrt{5-m}.$

Điều kiện để $y=sqrt{5 - m}.x - sqrt{5 - m}$

là hàm số hàm bậc nhất là:

$left{ matrix{ sqrt {5 - m} ne 0 hfill cr 5-m ge 0 hfill cr} right. Leftrightarrow left{ matrix{ 5-m ne 0 hfill cr 5-mge 0 hfill cr} right.$

$Leftrightarrow 5-m > 0 Leftrightarrow m < 5$

Vậy m < 5 thì hàm số đã cho là hàm số bậc nhất.

b) Ta có: $y = dfrac{m + 1}{m - 1}x +3,5 Rightarrow$

Hệ số $a=dfrac{m + 1}{m - 1}$

Điều kiện để hàm số $y = dfrac{m + 1}{m - 1}x +3,5$

là hàm bậc nhất là:

$left{ matrix{ dfrac{m + 1}{m - 1} ne 0 hfill cr m - 1 ne 0 hfill cr} right. Leftrightarrow left{ matrix{ m + 1 ne 0 hfill cr m - 1 ne 0 hfill cr} right. Leftrightarrow left{ matrix{ m ne - 1 hfill cr m ne 1 hfill cr} right.$

Vậy $m ne pm$

1 thì hàm số đã cho là hàm số bậc nhất.

Bài 14 (trang 48 SGK Toán 9 Tập 1)

Hàm số bậc nhất y = (1 – √5)x – 1.

READ Free Fire OB29: Thay đổi đặc biệt ở hệ thống pet

a) Hàm số trên là đồng biến hay nghịch biến trên R? Vì sao?

b) Tính giá trị của y khi x = 1 + √5.

c) Tính giá trị của x khi y = √5

Gợi ý đáp án

a) Ta có a = 1- √5 < 0 nên hàm số đã cho nghịch biến trên R.

b) Khi x = 1 + √5 ta có:

y = (1 – √5).(1 + √5) – 1 = (1 – 5) – 1 = -5

c) Khi y = √5 ta có:

√5 = (1 – √5)x – 1

=> √5 + 1 = (1 – √5)x

Giải bài tập SGK Toán 9 Tập 1 trang 48 để xem gợi ý giải các bài tập của Bài 2: Hàm số bậc nhất thuộc chương 2 Đại số 9.

Lý thuyết Hàm số bậc nhất

1. Định nghĩa

– Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b trong đó a, b là các số thực cho trước và a ≠ 0

– Đặc biệt, khi b = 0 thì hàm số bậc nhất trở thành hàm số y = ax, biểu thị tương quan tỉ lệ thuận giữa y và x

2. Tính chất

a) Hàm số bậc nhất y = ax + b xác định với mọi giá trị x ∈ R

b) Trên tập hợp số thực R, hàm số y = ax + b đồng biến khi a > 0 và nghịch biến khi a < 0

Hàm số y = f(x) gọi là đồng biến trong khoảng nào đó nếu với mọi x₁ và x₂ trong khoảng đó sao cho x₁ < x₂ thì f(x₁ ) < f(x₂ )

Hàm số y = f(x) gọi là nghịch biến trong khoảng nào đó nếu với mọi x₁ và x₂ trong khoảng đó sao cho x₁ < x₂ thì f(x₁ ) > f(x₂ )

3. Nhận xét về đồ thị hàm số y = ax + b (a ≠ 0)

Đồ thị của hàm số bậc nhất y = ax + b (a ≠ 0) còn gọi là đường thẳng y = ax + b; b được gọi là tung độ gốc của đường thẳng.