Home
Công thức tính thể tích khối tròn xoay | Vuidulich.vn

Công thức tính thể tích khối tròn xoay | Vuidulich.vn

3 Tháng mười, 2021 TIN TỨC Không có bình luận

Or you want a quick look: 1. Khối tròn xoay là gì?

Khối tròn xoay được tạo thành khi quay một hình phẳng quanh 1 đường cố định (trục quay) của hình đó. Vậy công thức tính thể tích khối tròn xoay như thế nào? Mời các bạn lớp 12 hãy cùng Mobitool theo dõi bài viết dưới đây nhé.

Ngoài ra các bạn lớp 12 tham khảo thêm 209 bài tập trắc nghiệm khối tròn xoay, Bài tập tự luận khối tròn xoay để có thêm nhiều tài liệu ôn tập nhé.

1. Khối tròn xoay là gì?

Trong không gian, khối tròn xoay là một khối hình được tạo bằng cách quay một mặt phẳng quanh một trục cố định.

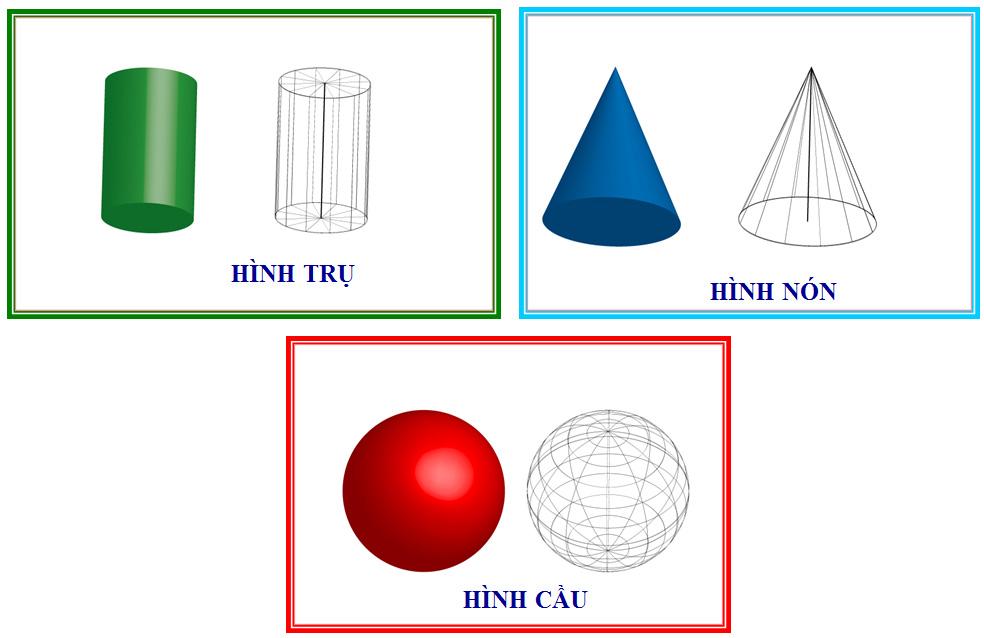
Trong chương trình toán học phổ thông các bạn sẽ được tiếp xúc với một số khối tròn xoay như khối nón tròn xoay, khối trụ tròn xoay, khối cầu tròn xoay,…

2. Tính thể tích khối tròn xoay quanh trục ox

Nếu khối tròn xoay quanh trục Ox thì để tính thể tích khối tròn xoay có thể áp dụng các công thức sau:

READ  Tháng 1 tiếng Anh là gì? - JES | Vuidulich.vn

Trường hợp 1: Khối tròn xoay tạo bởi

  • Đường thẳng y=f(x)
  • Trục hoành mathrm{y}=0
  • x=a ; x=b

Khi đó công thức tính thể tích sẽ là:

V=pi int_{a}^{b} f^{2}(x) d x

Trường hợp 2: Khối tròn xoay được tạo bởi:

  • Đường thẳng y=f(x)
  • Đường thẳng y=g(x)
  • x=a ; x=b

Khi đó công thức tính thể tích khối tròn xoay sẽ là

V=pi int_{a}^{b}left[f^{2}(x)-g^{2}(x)right] d x(g(x) leq f(x) text { với } forall x in[a ; b])

3. Tính thể tích khối tròn xoay quanh trục Oy

Nếu khối tròn xoay quanh trục Oy thì để tính thể tích khối tròn xoay có thể áp dụng các công thức sau:

Trường hợp 1: Khối tròn xoay được tạo bởi:

  • Đường x=g(y)
  • Trục tung (mathrm{x}=0)
  • mathrm{y}=mathrm{c} ; mathrm{y}=mathrm{d}

Khi đó công thức tính thể tích khối tròn xoay sẽ là:

V=pi int_{c}^{d} g^{2}(y) d y

Trường hợp 2 : Khối tròn xoay được tạo bởi:

  • Đường x=f(y)
  • Đường x=g(y)
  • mathrm{y}=mathrm{c} ; mathrm{y}=mathrm{d}

Khi đó thể tích khối tròn xoay sẽ được tính theo công thức sau:

V=pi int_{c}^{d}left[f^{2}(y)-g^{2}(y)right] d y quad(g(y) leq f(y) v text { ới } forall y in[c ; d])

4. Ví dụ tích thể tích khối tròn xoay

Ví dụ 1: Cho khối tròn xoay được tạo bởi đường thẳngy=sqrt{x}

; y=x và quay quanh trục Ox, hãy tính thể tích khối tròn xoay thu được.

Giải:

Giải phương trình:sqrt{x}=x Leftrightarrow x in{0 ; 1}

Thể tích khối tròn xoay là:

V=pi int_{0}^{1} int(sqrt{x})^{2} d x-pi int_{0}^{1} int(x)^{2} d x=frac{pi}{6}(d v t t)

Ví dụ 2: Tính thể tích khối tròn xoay được tạo bởi các đường y=frac{2}{y}

; trục tung, mathrm{y}= 1 ; mathrm{y}=4

Giải:

Thể tích khối tròn xoay được tạo bởi các đường y=frac{2}{y}

; trục tung,   mathrm{y}= 1 ; mathrm{y}=4 là

V=pi int_{1}^{4}left(frac{2}{y}right)^{2} d y=int_{1}^{4} frac{4}{y^{2}} d y=-frac{4}{y} l_{1}^{4}=3(mathrm{~d} v t t)

Ví dụ 3: Tính thể tích khối tròn xoay được tạo bởi y=sqrt{x} ; y=-x+2 ; y=0

quanh quanh trục Oy

Giải

Ta viết lại các đường left{begin{array}{l}y geq 0 x=y^{2}end{array}, x=2-y, y=0right.

Khi đó thể tích khối tròn xoay được tính như sau

V=left|pi int_{0}^{1}(2-y)^{2}-left(y^{2}right)^{2} d yright|=frac{32 pi}{15}(mathrm{~d} v t t)

Khối tròn xoay được tạo thành khi quay một hình phẳng quanh 1 đường cố định (trục quay) của hình đó. Vậy công thức tính thể tích khối tròn xoay như thế nào? Mời các bạn lớp 12 hãy cùng Mobitool theo dõi bài viết dưới đây nhé.

READ  IOS 14.4.1 có gì mới: Game thủ có nên cập nhật?

Ngoài ra các bạn lớp 12 tham khảo thêm 209 bài tập trắc nghiệm khối tròn xoay, Bài tập tự luận khối tròn xoay để có thêm nhiều tài liệu ôn tập nhé.

1. Khối tròn xoay là gì?

Trong không gian, khối tròn xoay là một khối hình được tạo bằng cách quay một mặt phẳng quanh một trục cố định.

Trong chương trình toán học phổ thông các bạn sẽ được tiếp xúc với một số khối tròn xoay như khối nón tròn xoay, khối trụ tròn xoay, khối cầu tròn xoay,…

2. Tính thể tích khối tròn xoay quanh trục ox

Nếu khối tròn xoay quanh trục Ox thì để tính thể tích khối tròn xoay có thể áp dụng các công thức sau:

Trường hợp 1: Khối tròn xoay tạo bởi

  • Đường thẳng y=f(x)
  • Trục hoành mathrm{y}=0
  • x=a ; x=b

Khi đó công thức tính thể tích sẽ là:

V=pi int_{a}^{b} f^{2}(x) d x

Trường hợp 2: Khối tròn xoay được tạo bởi:

  • Đường thẳng y=f(x)
  • Đường thẳng y=g(x)
  • x=a ; x=b

Khi đó công thức tính thể tích khối tròn xoay sẽ là

V=pi int_{a}^{b}left[f^{2}(x)-g^{2}(x)right] d x(g(x) leq f(x) text { với } forall x in[a ; b])

3. Tính thể tích khối tròn xoay quanh trục Oy

Nếu khối tròn xoay quanh trục Oy thì để tính thể tích khối tròn xoay có thể áp dụng các công thức sau:

Trường hợp 1: Khối tròn xoay được tạo bởi:

  • Đường x=g(y)
  • Trục tung (mathrm{x}=0)
  • mathrm{y}=mathrm{c} ; mathrm{y}=mathrm{d}

Khi đó công thức tính thể tích khối tròn xoay sẽ là:

V=pi int_{c}^{d} g^{2}(y) d y

Trường hợp 2 : Khối tròn xoay được tạo bởi:

  • Đường x=f(y)
  • Đường x=g(y)
  • mathrm{y}=mathrm{c} ; mathrm{y}=mathrm{d}

Khi đó thể tích khối tròn xoay sẽ được tính theo công thức sau:

READ  Đánh giá nhanh Vega iRon 2 (SKY A910) - Di Động Thông Minh

V=pi int_{c}^{d}left[f^{2}(y)-g^{2}(y)right] d y quad(g(y) leq f(y) v text { ới } forall y in[c ; d])

4. Ví dụ tích thể tích khối tròn xoay

Ví dụ 1: Cho khối tròn xoay được tạo bởi đường thẳngy=sqrt{x}

; y=x và quay quanh trục Ox, hãy tính thể tích khối tròn xoay thu được.

Giải:

Giải phương trình:sqrt{x}=x Leftrightarrow x in{0 ; 1}

Thể tích khối tròn xoay là:

V=pi int_{0}^{1} int(sqrt{x})^{2} d x-pi int_{0}^{1} int(x)^{2} d x=frac{pi}{6}(d v t t)

Ví dụ 2: Tính thể tích khối tròn xoay được tạo bởi các đường y=frac{2}{y}

; trục tung, mathrm{y}= 1 ; mathrm{y}=4

Giải:

Thể tích khối tròn xoay được tạo bởi các đường y=frac{2}{y}

; trục tung,   mathrm{y}= 1 ; mathrm{y}=4 là

V=pi int_{1}^{4}left(frac{2}{y}right)^{2} d y=int_{1}^{4} frac{4}{y^{2}} d y=-frac{4}{y} l_{1}^{4}=3(mathrm{~d} v t t)

Ví dụ 3: Tính thể tích khối tròn xoay được tạo bởi y=sqrt{x} ; y=-x+2 ; y=0

quanh quanh trục Oy

Giải

Ta viết lại các đường left{begin{array}{l}y geq 0 x=y^{2}end{array}, x=2-y, y=0right.

Khi đó thể tích khối tròn xoay được tính như sau

V=left|pi int_{0}^{1}(2-y)^{2}-left(y^{2}right)^{2} d yright|=frac{32 pi}{15}(mathrm{~d} v t t)

See more articles in the category: TIN TỨC

About The Author

admin

Leave a Reply